最終更新日：2022年11月6日

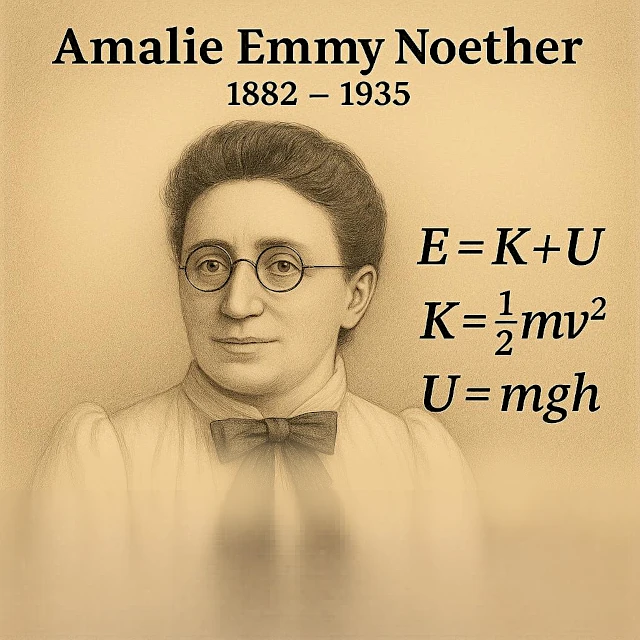
ネーターの定理の魔法：最小作用の原理から保存則へ

最小作用の原理

最小作用の原理は、自然は常に「作用」と呼ばれる量を最小化する経路をたどると述べています。 17世紀にピエール・ド・フェルマ（1607-1665）によって光に関して最初に観察され、18世紀にジョゼフ＝ルイ・ラグランジュ（1736-1813）によって形式化され、ネーターの定理の基礎を築きました。

最小作用の原理は、運動エネルギーと位置エネルギーの差（K-U）からシステムの運動を決定し、振り子から銀河まであらゆる物理システムのダイナミクスを予測することを可能にします。

ネーターの定理の主張

「作用積分を不変に保つ無限小変換には、保存される量が対応する。」

この主張の背後にあるものは何か？

物理法則が、システムに小さな変換（移動、回転、時間の進行）を加えたときに同じままである場合、特定の物理量（エネルギー、運動量、電荷など）が一定のまま変化しないものが存在します。

このように、ネーターは、各対称性に保存則が対応することを確立しました。

対称性とは何か？

対称性は、自然法則における不変性を記述します。それらは単に美的なものではなく、物理学の多くの基本原理の基礎を形成しています。

物理学において、対称性とは、システムの振る舞いの法則が、並進、回転、時間の変化などの特定の変換を加えたときに変化しない性質のことです。

保存則に対応する対称性

空間並進不変性：運動量の保存。
回転不変性：角運動量の保存。
時間不変性：エネルギーの保存。
電磁気学的ゲージ対称性：電荷の保存。
色ゲージ対称性：色荷の保存（量子色力学）。
弱いゲージ不変性：レプトン数とバリオン数の保存。
CPT対称性（電荷、パリティ、時間）：量子場理論の基本的不変性。
大域的位相変換不変性：粒子数の保存。
アイソスピン対称性：強い相互作用におけるアイソスピンの保存。
ローレンツ不変性：エネルギー運動量四元ベクトルの保存。

これらの対称性は、宇宙の基本的な性質を証明しています：物理法則は普遍的かつ不変であり、空間的位置、時間的瞬間、選択された方向、または量子場に適用されるゲージ変換に依存しません。

具体的には、これは数十億年前に同じ原理が物質を支配し、遠い未来にも適用され続けることを意味します。赤道で行われる実験は、北極で行われる実験と同じ結果をもたらします。同様に、システムの空間的な向きはそのダイナミクスに影響を与えないため、太陽系形成以来、惑星軌道が安定したままである理由を説明します。

ネーターの定理を振り子に適用する

静かに振動する単純な振り子を観察しましょう。その総機械的エネルギーEは、運動に関連する運動エネルギーKと位置に関連する位置エネルギーUの2つの異なるが密接に関連した形に分解され、方程式E = K + Uで表されます。

振り子が運動しているとき、その運動エネルギーはK = ½mv²で表されます。速く動くほど（vが大きいほど）このエネルギーは大きくなります。これは、速度が最大になる振り子の最下点でピークに達します。

逆に、重力による位置エネルギーU = mghは、振り子の高さhに依存します。振り子の振動の端で、平衡位置より上に上がると、この蓄えられたエネルギーは最大になり、速度はゼロになります。

ネーターの定理と物理法則の時間的不変性により、総エネルギーEは厳密に一定のままであることがわかります。振り子は、2つのエネルギー形態の間で永続的な変換を行います：下降するとき、位置エネルギーを運動エネルギーに変換し、上昇するとき、運動エネルギーを再び位置エネルギーに変換します。このエネルギーのバレエは、対称性（ここでは時間的）が保存則（エネルギーの）を生み出す方法を具体的に示しています。