最終更新：2024年8月29日

量子不確定性の重要な役割：どの粒子も静止することはできない

アインゼンベルクの公式

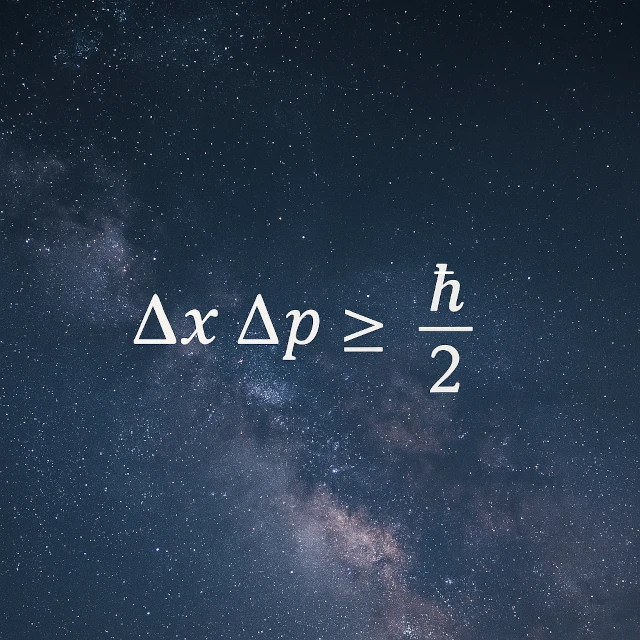
アインゼンベルクの公式は量子力学の基本的な発見です。 1927年にヴェルナー・アインゼンベルク（1901-1976）によって定式化され、位置（x）や運動量（p）などの物理的性質のペアを同時に知ることができる精度に基本的な限界があることを表しています。

この関係は数学的に不等式で表されます：Δx * Δp ≥ ħ/2、ここで\(\hbar = \frac{h}{2\pi}\)（hはプランク定数、ħは約1.054 × 10⁻³⁴ J·sのプランク定数の約半分）。不等式（≥）は、二つの不確定性（Δx）と（Δp）の積がħ/2を下回ることは決してないことを意味します。

つまり：粒子の位置（Δx）を精密に測定すればするほど、その運動量（Δp）を精密に知ることはできなくなり、その逆も同様です。これは自然の基本的な限界であり、我々の測定器具の技術的な限界ではありません。量子粒子の位置と速度を同時に絶対的な精度で知ることは決してできません。

Δx * Δp ≥ ħ/2の用語の解釈

左側：Δx * Δp

Δx（デルタx）は粒子の位置の不確定性を表します。これは、粒子が空間内のどこにあるかを正確に知る際の「誤差の余地」または不精確さです。 Δp（デルタp）は粒子の運動量（またはインパルス）の不確定性を表します。運動量p = mv（質量×速度）なので、Δpは粒子の速度/運動の不精確さを測定します。したがって、Δx * Δpはこれら二つの不確定性の積を表します。

右側：ħ/2

ħ（エイチバー）は約1.054 × 10⁻³⁴ J·sのプランク定数hを2πで割ったもので、量子スケールを特徴づける自然の基本定数です。 ħ/2はこの定数の半分です。

我々のスケールでは知覚できない限界

ħの小ささは、我々のマクロスケールで物体の位置と運動を「知っている」ことを意味するものではありません。それは、我々の通常の測定の不精確さがħ/2に比べて非常に大きく、マクロスケールの物体の量子効果を隠していることを意味します。この不等式は常に実践的に広く検証されています。

量子スケールでは、我々の測定精度は10⁻¹⁵ mのオーダーであり、ħ/2からはるかに遠いです。変わるのは、ħ/2によって課せられる妥協が粒子の振る舞いを理解するために関連してくることです。不確定性原理は、電子を10⁻¹⁰ m（原子の大きさ）の空間に閉じ込めると、自動的に運動を持つことになり、Δxを減らすとΔxΔp ≥ ħ/2の関係に従ってΔpを増やさなければならないため、このスケールで物理的に意味を持ちます。
したがって、静止した局在電子は不可能であり、これがどの粒子も静止できない理由を説明しています。

ハイゼンベルクの不確定性原理のアイデアを視覚化するための例

高速で走行する車の非常に鮮明な写真を撮ろうとしていると想像してください。鮮明な画像を得るためには、非常に短い露出時間を使用する必要があります。しかし、短い露出時間は光を少なく捕らえることを意味し、光が不十分な場合、画像が暗くまたはぼやける可能性があります。

正確な位置（鮮明な写真）：車の非常に鮮明な写真を撮ることができた場合、その瞬間の車の位置を捉えたことになります。しかし、露出時間が短いため、車の運動（速度）に関する情報は少なくなります。なぜなら、移動の文脈のない瞬間的なスナップショットしか見えないからです。
正確な運動（ぼやけた写真）：より多くの光を捕らえて明るい画像を得るために長い露出時間を使用すると、露出中の車の運動により車がぼやけて見えます。この場合、運動に関する情報（ぼやけが方向と速度を示す）は多くなりますが、特定の瞬間における車の正確な位置の精度は失われます。

現代物理学への影響

量子スケールでの現実：不確定性原理により、システムの進化を正確に予測することが可能になりました。この原理は、量子スケールでの現実が本質的に確率論的であることを示しています。古典物理学の決定論的な視点を確率論的な枠組みに置き換えました。
波動関数の収縮：不確定性は、ある量を測定することがシステムを乱す可能性があり、「客観的な観測者」の概念を問題視させます。「波動関数の収縮」の概念は、測定がシステムの波動関数を定義された状態に「収縮」させると仮定し、不確定性原理の結果として一部生じました。
エネルギーの量子化：不確定性原理は、原子（ボーアモデル）や分子などのシステムにおけるエネルギーの量子化などの現象を説明するために不可欠です。量子効果は、超伝導や超流動などのマクロな現象に影響を与えます。
トンネル効果：不確定性原理は、トンネル効果を説明するためにも基本的です。トンネル効果は、粒子が古典物理学の法則によればエネルギーバリアを越えるのに十分なエネルギーを持っていない場合でも、エネルギーバリアを通過する非ゼロの確率を持つ量子現象です。この現象は、トンネル効果トランジスタやトンネル効果顕微鏡などのデバイスで利用されています。
量子真空：不確定性のため、量子真空（システムの基底状態）でさえ完全に「空」ではなく、量子ゆらぎの影響を受けます。
波動と粒子の二重性：不確定性は、電子や光子などの量子物体が波動と粒子の両方として振る舞うことを説明する波動と粒子の二重性と密接に関連しています。位置と運動量の不確定性は、この二重性の直接的な現れです。