Coulomb vs. Newton: Die rätselhafte Ähnlichkeit der Kräfte des Universums

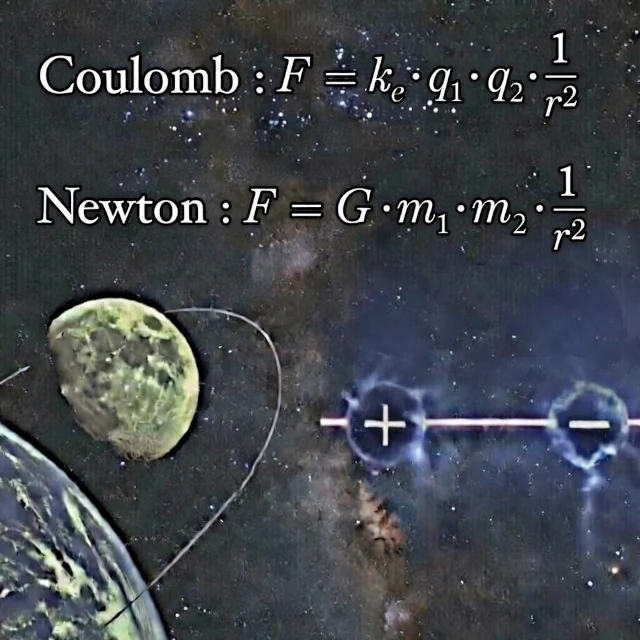
Visueller Vergleich zwischen der gravitativen Anziehung der Planeten und der elektrostatischen Abstoßung von Ladungen — Illustration der mathematischen Analogie zwischen der gravitativen Anziehung, die die Erde mit dem Mond verbindet, und der elektrostatischen Kraft, die zwischen zwei entgegengesetzten Ladungen wirkt. In beiden Fällen nimmt die Intensität der Wechselwirkung gemäß einem Quadratgesetz der Entfernung ab, eine tiefe mathematische Struktur, die kein Zufall ist.
Bildquelle: astronoo.com (neues Fenster)

Zwei Kräfte, eine mathematische Struktur

Warum umkreist der Mond die Erde? Warum stellen sich Ihre Haare auf, nachdem Sie eine Wollmütze abgezogen haben? Die Antwort auf diese beiden scheinbar so unterschiedlichen Fragen ist in fast identischen mathematischen Strukturen geschrieben. Auf der einen Seite das Gesetz der universellen Gravitation, formuliert von Isaac Newton (1643-1727) am Ende des 17. Jahrhunderts. Auf der anderen Seite das Gesetz der Elektrostatik, aufgestellt von Charles-Augustin de Coulomb (1736-1806) am Ende des 18. Jahrhunderts. Beide sind "Quadratgesetze der Entfernung".

Für die Gravitation: \( F_g = G \cdot \frac{m_1 \cdot m_2}{r^2} \)
Für die Elektrizität: \( F_e = k_e \cdot \frac{q_1 \cdot q_2}{r^2} \)

In diesen Gleichungen steht \( F \) für die Kraft, \( m \) für die Masse, \( q \) für die elektrische Ladung und \( r \) für den Abstand zwischen den beiden Objekten. Die Konstanten \( G \) und \( k_e \) sind lediglich Skalierungsfaktoren. Ist diese auffällige Ähnlichkeit ein kosmischer Zufall oder ein Zeichen einer tieferen Wahrheit über die Struktur des Universums?

Das geometrische Geheimnis des dreidimensionalen Raums

Der grundlegendste Grund für diese Ähnlichkeit ist geometrisch.

Wir leben in einem dreidimensionalen Raum. Stellen Sie sich eine punktförmige Einflussquelle vor, sei es eine Masse oder eine Ladung. Dieser Einfluss breitet sich kugelförmig und isotrop (in allen Richtungen identisch) um sie herum aus.

In einem Abstand \( r \) von der Quelle muss der gesamte ausgeübte Einfluss eine imaginäre kugelförmige Oberfläche durchqueren. Warum eine Oberfläche und kein Volumen? Weil sich der Einfluss wie eine kugelförmige Wellenfront ausbreitet. Zu einem gegebenen Zeitpunkt werden alle Punkte, die sich in derselben Entfernung \( r \) von der Quelle befinden, gleichzeitig erreicht. Diese Punkte bilden genau eine kugelförmige Oberfläche, kein Volumen.

Geometrische Verdünnung des Einflusses

Die Oberfläche einer Kugel ist durch die Formel \( 4\pi r^2 \) gegeben. Die Energie oder Intensität der Wirkung (die man als Fluss bezeichnet) verteilt sich daher gleichmäßig über diese Oberfläche, während sie sich von der Quelle entfernt.

Wenn die Quelle eine Gesamtmenge an Einfluss pro Sekunde ausstrahlt, die wir \( Q \) nennen (eine Flussrate), dann ist die Intensität \( I \), die an einem Punkt in der Entfernung \( r \) gemessen wird, diese Gesamtmenge geteilt durch die Oberfläche, über die sie sich ausbreitet: \( I = \frac{Q}{4\pi r^2} \)

Die Kerzenanalogie

Dieser Ausdruck bedeutet, dass je weiter man sich entfernt, desto größer die zu durchquerende Oberfläche ist (\( 4\pi r^2 \) nimmt mit \( r \) zu), und damit die Intensität pro Flächeneinheit abnimmt. Es ist genau wie das Licht einer Kerze: in 1 Meter Entfernung beleuchtet es eine bestimmte Fläche; in 2 Metern Entfernung muss dieselbe Lichtmenge eine 4-mal größere Fläche beleuchten (da \( (2)^2 = 4 \)), so dass die Lichtintensität pro Flächeneinheit 4-mal schwächer ist.

Oberfläche und nicht Volumen: die richtige physikalische Größe

Das Volumen spielt hier keine Rolle, weil wir eine Wirkung an einem Punkt der Oberfläche messen, nicht in einem dreidimensionalen Raum. Die relevante physikalische Größe ist die Flussdichte pro Fläche, nicht eine Volumendichte.

Mathematische Zerlegung

Dieser Ausdruck zerfällt in zwei Teile:
- \( Q \) ist eine Konstante, die nur von der Quelle abhängt (ihre Emissionsleistung).
- \( \frac{1}{4\pi r^2} \) ist ein geometrischer Faktor, der beschreibt, wie sich der Einfluss auf einer kugelförmigen Oberfläche verdünnt.

Mathematisch können wir umschreiben: \( I = \left( \frac{Q}{4\pi} \right) \times \frac{1}{r^2} \)

Der Term \( \frac{Q}{4\pi} \) ist eine globale Konstante für eine gegebene Quelle. Die Abhängigkeit von der Entfernung ist daher vollständig im Faktor \( \frac{1}{r^2} \) enthalten. Daher sagt man, dass die Intensität umgekehrt proportional zum Quadrat der Entfernung ist.

Anwendung auf die Gesetze von Coulomb und Newton

In den Gesetzen von Coulomb und Newton finden wir diese gleiche Struktur:
- Für Coulomb: \( F = k_e \cdot q_1 \cdot q_2 \cdot \frac{1}{r^2} \)
- Für Newton: \( F = G \cdot m_1 \cdot m_2 \cdot \frac{1}{r^2} \)

Die Konstanten \( k_e \) und \( G \) integrieren bereits geometrische Faktoren wie \( \frac{1}{4\pi} \) (im geeigneten Einheitensystem, wie dem rationalisierten SI-System), sowie die grundlegenden Eigenschaften der Wechselwirkung.

Was wäre, wenn der Raum andere Dimensionen hätte?

Wenn wir in einem zweidimensionalen Universum leben würden, würde sich der Einfluss über einen Kreis (einen Umfang) der Länge \( 2\pi r \) verteilen, und das Gesetz würde zu \( I = \frac{Q}{2\pi r} = \left( \frac{Q}{2\pi} \right) \times \frac{1}{r} \), also ein \( 1/r \)-Gesetz. In vier Dimensionen würde es einem \( 1/r^3 \)-Gesetz folgen. Das Quadratgesetz ist daher die mathematische Signatur einer Kraft, die sich in einem dreidimensionalen Raum ausbreitet.

Aber das Universum ist nicht so einfach

Obwohl die mathematische Form identisch ist, ist die tiefe Natur dieser beiden Kräfte radikal unterschiedlich. Der erste Unterschied liegt auf der Hand: Masse ist immer positiv, daher ist Gravitation immer anziehend. Elektrische Ladungen können hingegen positiv oder negativ sein. Die elektrische Wechselwirkung kann daher sowohl anziehend als auch abstoßend sein.

Das Doppelleben des Coulomb-Gesetzes

Das Coulomb-Gesetz hat also zwei komplementäre Gesichter, die unsere Realität strukturieren:

Anziehung zwischen entgegengesetzten Ladungen hält die Elektronen um den Kern und bildet Atome.
Abstoßung zwischen gleichen Ladungen verhindert, dass diese Atome verschmelzen, und verleiht der Materie ihre feste Konsistenz (Ihre Hand kann nicht durch einen Tisch gehen).

Diese Dualität macht das Coulomb-Gesetz zu einem der elegantesten und fundamentalsten Pfeiler der Physik. Ohne sie wäre das Universum nur eine undifferenzierte Teilchensuppe, ohne Struktur, ohne Leben und ohne Tisch, auf den Sie Ihre Hand legen können.

Der zweite Unterschied liegt in der Intensität. Die elektrische Kraft ist unvorstellbar stärker als die Gravitationskraft. Um sich davon zu überzeugen, vergleichen Sie die elektrische Abstoßungskraft zwischen zwei Protonen mit ihrer Gravitationsanziehungskraft. Das Verhältnis beträgt etwa \( 10^{36} \) zugunsten der Elektrizität. Wenn die Gravitation auf der Ebene von Planeten und Galaxien dominiert, dann nur, weil Materie auf großer Skala elektrisch neutral ist. Positive und negative Ladungen heben sich auf und lassen nur die schwache, aber allgegenwärtige Gravitation übrig.

Vergleichstabelle der beiden Grundkräfte

Vergleich des Coulomb-Gesetzes und des Newtonschen Gesetzes
Eigenschaft	Gravitation (Newton)	Elektrostatik (Coulomb)
Quelle	Masse (immer positiv)	Elektrische Ladung (positiv oder negativ)
Art der Kraft	Immer anziehend	Anziehend oder abstoßend
Konstante	\( G = 6,674 \times 10^{-11} \, \text{N·m}^2/\text{kg}^2 \)	\( k_e = 8,988 \times 10^9 \, \text{N·m}^2/\text{C}^2 \)
Relative Intensität	\( 10^{-36} \) (die schwächste)	\( 10^{36} \) (viel stärker)
Abschirmung	Unmöglich (keine negative Masse)	Möglich (elektrische Neutralität)
Dominanzbereich	Astronomisch (Planeten, Galaxien)	Atomar und molekular

Die Synthese der Kräfte

Diese Ähnlichkeit hat die größten Geister fasziniert. Albert Einstein (1879-1955) verbrachte die letzten dreißig Jahre seines Lebens damit, Gravitation und Elektromagnetismus in einer einzigen Theorie zu vereinen, einer "vereinheitlichten Feldtheorie". Er scheiterte, aber seine Suche ebnete den Weg für die moderne Physik. Heute wissen wir, dass diese beiden Kräfte Niedrigenergie-Manifestationen tieferer Theorien sind.

Die Gravitation wird durch die allgemeine Relativitätstheorie als Krümmung der Raumzeit beschrieben. Der Elektromagnetismus, zu dem die Elektrostatik gehört, wird durch die Quantenelektrodynamik beschrieben. Die Vereinheitlichung dieser beiden Säulen (allgemeine Relativitätstheorie und Quantenmechanik) bleibt der Heilige Gral der theoretischen Physik, eine Suche danach, warum diese beiden so unterschiedlichen Kräfte auf fundamentaler Ebene diese elegante mathematische Struktur teilen.