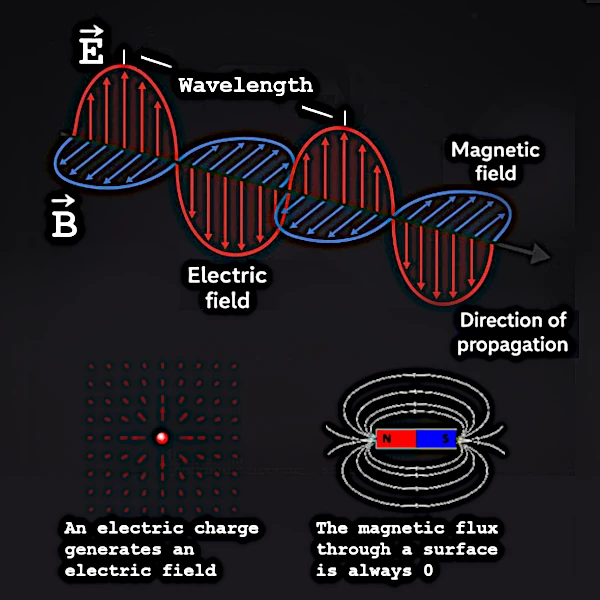
All electromagnetic phenomena can be reduced to a system of four fundamental relations: Maxwell's equations. These equations alone predict everything about the dynamics of electric and magnetic fields.
The last two equations are the key to the mystery of the runaway. A time-varying magnetic field (\( \partial \mathbf{B}/\partial t \)) creates a rotating electric field. Symmetrically, a time-varying electric field (\( \partial \mathbf{E}/\partial t \)) creates a rotating magnetic field. It is this dynamic coupling that self-sustains throughout their propagation.
When James Clerk Maxwell (1831–1879) unified the laws of electricity and magnetism in the 19th century, he discovered a surprising phenomenon: a local disturbance of an electric or magnetic field creates a wave that propagates on its own in a vacuum, without the need for additional energy.
Maxwell showed that this wave travels at a finite speed, determined by two properties of the vacuum:
The formula \( c = \frac{1}{\sqrt{\mu_0 \varepsilon_0}} \) gives this speed.
By combining Faraday's and Ampère-Maxwell's laws, he obtained a wave equation. By plugging in the values of μ₀ and ε₀, he found: \( c \approx 300,000 \) km/s, the speed of light!
In 1865, Maxwell concluded that light is an electromagnetic wave, just like radio waves or microwaves. A discovery that revolutionized physics.
N.B.:
At the time of Maxwell (1865), the speed of light was not yet known with great precision. The experimental measurements available, carried out notably by Armand Fizeau (1819-1896) and Albert Michelson (1852-1931), allowed estimating \( v \) with a significant margin of error. Maxwell's theoretical calculation thus gave a value very close to what would later be confirmed, which constituted an impressive validation of his theory.
When Maxwell assembled the laws of electricity and magnetism, he discovered a self-sustaining structure, as soon as an electric or magnetic field is locally disturbed. This "runaway" is stable, without amplification, and has no internal energy source. The vacuum carries the wave without feeding it.
This dynamic loop between \( \mathbf{B} \) and \( \mathbf{E} \), produces a structure that propagates in the vacuum at finite speed.
The term \(\mu_0 \varepsilon_0\) of the fourth equation sets the speed of light: \( c = \frac{1}{\sqrt{\mu_0 \varepsilon_0}}. \)
By mathematically combining Faraday's and Ampère-Maxwell's laws (by taking the curl of one and using the other), the coupling is eliminated to obtain an equation describing each field alone.
For the electric field, we find: \( \nabla^2 \mathbf{E} = \mu_0 \varepsilon_0 \frac{\partial^2 \mathbf{E}}{\partial t^2} \) This is the classic form of the wave equation. The term \( \mu_0 \varepsilon_0 \) is in front of the second time derivative. In mathematical physics, the standard wave equation is written as \( \nabla^2 \psi = \frac{1}{v^2} \frac{\partial^2 \psi}{\partial t^2} \), where \( v \) is the propagation speed.
By immediate identification: \( \frac{1}{v^2} = \mu_0 \varepsilon_0 \quad \Rightarrow \quad v = \frac{1}{\sqrt{\mu_0 \varepsilon_0}} \)
Maxwell calculated this value with the constants known in his time:
The result is astonishing: \( v \approx 2.998 \times 10^{8} \, \text{m/s} \), the speed of the waves corresponds to the speed of light measured experimentally!
N.B.:
This mathematical demonstration assumes a vacuum, i.e., the absence of charges and currents (\( \rho = 0, \, \mathbf{J} = 0 \)). The reasoning consists in taking the curl of Faraday's law and using the vector identity \( \nabla \times (\nabla \times \mathbf{E}) = \nabla(\nabla \cdot \mathbf{E}) - \nabla^2 \mathbf{E} \), combining with Gauss's law (\( \nabla \cdot \mathbf{E} = 0 \) in a vacuum) and the Ampère-Maxwell law. We thus obtain the same wave equation for the magnetic field \( \mathbf{B} \). This theoretical prediction by James Clerk Maxwell (1831-1879) in 1865 was experimentally confirmed by Heinrich Hertz (1857-1894) in 1887, when he produced the first radio waves.
Maxwell found that electromagnetic waves propagate at a certain speed in a vacuum, but the demonstration that this is a limiting speed was not yet established. Maxwell did not yet know relativity. He therefore had no reason to think that it was a universal limiting speed. The notion of a universal limit only appeared with special relativity, long after Maxwell.
It was only with special relativity (1905) by Albert Einstein (1879-1955) that the speed of light in a vacuum \( c \) was recognized as the maximum speed at which information, energy, or any physical interaction can propagate. In other words, \( c \) is a fundamental limit imposed by the structure of spacetime, and not just a consequence of Maxwell's equations.
Electromagnetic phenomena obey Maxwell's equations and can be summarized as follows:
Thus, light and all electromagnetic waves are nothing but the manifestation of this phenomenon of self-sustaining electric and magnetic fields in a vacuum.
Electromagnetic Runaway: The Secret of the Speed of Light 
Understanding the Photoelectric Effect: Light and Electrons 
How far is the horizon? 
How Do Solar Panels Inject Electricity into the Grid? 
Dynamics of Momentum to explain the propulsion of rockets or jellyfish 
Energy Distribution of Electrons in Atoms 
Heisenberg's Uncertainty Principle: Understanding Quantum Uncertainty 
Relation between Energy, Power, and Time 
Why is there a limit to cold, but not to heat? 
Galileo's Law of Falling Bodies 
The Ideal Gas Law 
Schrödinger Equation and Atomic Structure 
Noether's Theorem: conservation of energy follows from symmetries 
Relationship
between gravitational mass and inertial mass and the equivalence principle 
The Third Essential Equation
in Physics 
The Second Essential Equation
in Physics 
The first essential equation
in physics 
The electromagnetic force or Lorentz force 
The solar energy received depends on
the angle of incidence 
Why is marble colder
than wood? 
Why does a photon, which has no mass, have energy?
Bayes Formula and Artificial
Intelligence 
The seven fundamental constants of physics 
What temperature does it feel like in interstellar space? 
Black body radiation curves: Planck's law 
The equivalence principle, gravitational effects are indistinguishable from acceleration 
E=mc2: The four fundamental concepts of the universe revisited 
How to weigh the sun? 
Equation of the free fall of bodies (1604) 
Coulomb's equation (1785) 
Boltzmann's equationon entropy (1877) 
Special relativity equations (1905) 
The equation of general relativity (1915) 
Planetary Rotation Equations: Between Angular Momentum and Gravitational Balance 
Equation of the orbital velocity of a planet 
Planck's equation 
Schrödinger's equation 
How Newton's Three Laws Describe All of Classical Mechanics 
Maxwell's equations 
Paul Dirac's equation 
Conservation of energy 
Equation of electromagnetic induction 
Why do elementary particles have no mass? 
Difference between heat and temperature