Todos os fenômenos eletromagnéticos podem ser reduzidos a um sistema de quatro relações fundamentais: as equações de Maxwell. Sozinhas, essas equações preveem tudo sobre a dinâmica dos campos elétricos e magnéticos.
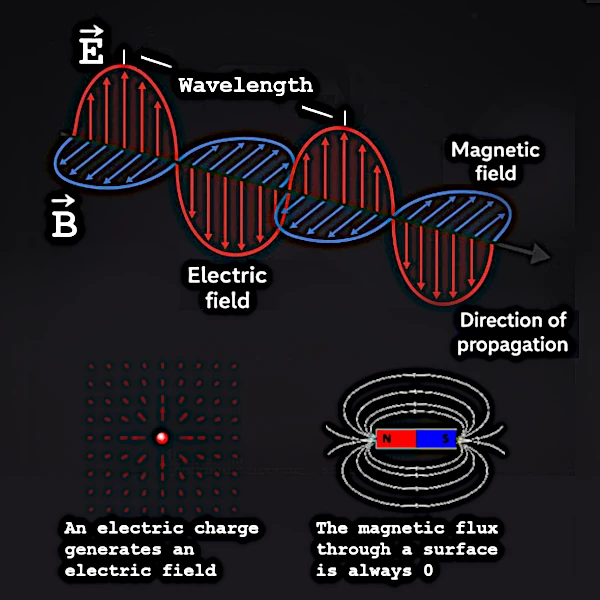
As duas últimas equações são a chave do mistério do embalamento. Um campo magnético variável no tempo (\( \partial \mathbf{B}/\partial t \)) cria um campo elétrico rotativo. Simetricamente, um campo elétrico variável (\( \partial \mathbf{E}/\partial t \)) cria um campo magnético rotativo. É esse acoplamento dinâmico que se auto-sustenta ao longo de sua propagação.
Quando James Clerk Maxwell (1831–1879) unificou as leis da eletricidade e do magnetismo no século XIX, ele descobriu um fenômeno surpreendente: uma perturbação local de um campo elétrico ou magnético cria uma onda que se propaga sozinha no vácuo, sem necessidade de energia adicional.
Maxwell mostrou que esta onda se move a uma velocidade finita, determinada por duas propriedades do vácuo:
A fórmula \( c = \frac{1}{\sqrt{\mu_0 \varepsilon_0}} \) dá esta velocidade.
Ao combinar as leis de Faraday e de Ampère-Maxwell, ele obteve uma equação de onda. Ao inserir os valores de μ₀ e ε₀, ele encontrou: \( c \approx 300.000 \) km/s, a velocidade da luz!
Em 1865, Maxwell concluiu que a luz é uma onda eletromagnética, assim como as ondas de rádio ou micro-ondas. Uma descoberta que revolucionou a física.
N.B.:
Na época de Maxwell (1865), a velocidade da luz ainda não era conhecida com grande precisão. As medições experimentais disponíveis, realizadas notavelmente por Armand Fizeau (1819-1896) e Albert Michelson (1852-1931), permitiam estimar \( v \) com uma margem de erro significativa. O cálculo teórico de Maxwell deu, portanto, um valor muito próximo do que seria confirmado mais tarde, o que constituiu uma validação impressionante da sua teoria.
Quando Maxwell reuniu as leis da eletricidade e do magnetismo, ele descobriu uma estrutura auto-sustentável, assim que um campo elétrico ou magnético é localmente perturbado. Este "embalamento" é estável, sem amplificação, e não possui nenhuma fonte interna de energia. O vácuo transporta a onda sem alimentá-la.
Este loop dinâmico entre \( \mathbf{B} \) e \( \mathbf{E} \), produz uma estrutura que se propaga no vácuo a uma velocidade finita.
O termo \(\mu_0 \varepsilon_0\) da quarta equação define a velocidade da luz: \( c = \frac{1}{\sqrt{\mu_0 \varepsilon_0}}. \)
Ao combinar matematicamente as leis de Faraday e de Ampère-Maxwell (tomando o rotacional de uma e usando a outra), o acoplamento é eliminado para obter uma equação que descreve cada campo separadamente.
Para o campo elétrico, encontramos: \( \nabla^2 \mathbf{E} = \mu_0 \varepsilon_0 \frac{\partial^2 \mathbf{E}}{\partial t^2} \) Esta é a forma clássica da equação de onda. O termo \( \mu_0 \varepsilon_0 \) está na frente da derivada segunda temporal. Em física matemática, a equação de onda padrão é escrita como \( \nabla^2 \psi = \frac{1}{v^2} \frac{\partial^2 \psi}{\partial t^2} \), onde \( v \) é a velocidade de propagação.
Por identificação imediata: \( \frac{1}{v^2} = \mu_0 \varepsilon_0 \quad \Rightarrow \quad v = \frac{1}{\sqrt{\mu_0 \varepsilon_0}} \)
Maxwell calculou este valor com as constantes conhecidas em sua época:
O resultado é surpreendente: \( v \approx 2.998 \times 10^{8} \, \text{m/s} \), a velocidade das ondas corresponde à velocidade da luz medida experimentalmente!
N.B.:
Esta demonstração matemática supõe o vácuo, ou seja, a ausência de cargas e correntes (\( \rho = 0, \, \mathbf{J} = 0 \)). O raciocínio consiste em tomar o rotacional da lei de Faraday e usar a identidade vetorial \( \nabla \times (\nabla \times \mathbf{E}) = \nabla(\nabla \cdot \mathbf{E}) - \nabla^2 \mathbf{E} \), combinando com a lei de Gauss (\( \nabla \cdot \mathbf{E} = 0 \) no vácuo) e a lei de Ampère-Maxwell. Assim, obtemos a mesma equação de onda para o campo magnético \( \mathbf{B} \). Esta previsão teórica de James Clerk Maxwell (1831-1879) em 1865 foi confirmada experimentalmente por Heinrich Hertz (1857-1894) em 1887, quando produziu as primeiras ondas de rádio.
Maxwell descobriu que as ondas eletromagnéticas se propagam a uma certa velocidade no vácuo, mas a demonstração de que esta é uma velocidade limite ainda não estava estabelecida. Maxwell ainda não conhecia a relatividade. Portanto, não tinha nenhuma razão para pensar que era uma velocidade limite universal. A noção de limite universal só apareceu com a relatividade restrita, muito depois de Maxwell.
Foi somente com a relatividade restrita (1905) de Albert Einstein (1879-1955) que a velocidade da luz no vácuo \( c \) foi reconhecida como a velocidade máxima na qual a informação, a energia ou qualquer interação física pode se propagar. Em outras palavras, \( c \) é um limite fundamental imposto pela estrutura do espaço-tempo, e não apenas uma consequência das equações de Maxwell.
Os fenômenos eletromagnéticos obedecem às equações de Maxwell e podem ser resumidos da seguinte forma:
Assim, a luz e todas as ondas eletromagnéticas não são nada além da manifestação desse fenômeno de auto-sustentação dos campos elétricos e magnéticos no vácuo.
O Embalamento Eletromagnético: O Segredo da Velocidade da Luz 
Compreender o Efeito Fotoelétrico: A Luz e os Eletrões 
A que distância fica o horizonte? 
Como os Painéis Solares Injetam Eletricidade na Rede? 
Dinâmica do Momentum para explicar a propulsão de foguetões ou medusas 
Distribuição Energética dos Elétrons em Átomos 
Princípio da Incerteza de Heisenberg: Compreendendo a Incerteza Quântica 
Relação entre Energia, Potência e Tempo 
Por que existe um limite para o frio, mas não para o calor? 
A Lei da Queda dos Corpos de Galileu 
A Lei dos Gases Ideais 
Equação de Schrödinger e Estrutura dos Átomos 
Teorema de Noether: a conservação da energia surge de simetrias 
Relação entre massa gravitacional e massa inercial e o princípio da equivalência 
A Terceira Equação Essencial em Física 
A Segunda Equação Essencial em Física 
A primeira equação essencial em física 
A força eletromagnética ou força de Lorentz 
A energia solar recebida varia dependendo da inclinação 
Por que o mármore é mais frio que a madeira? 
Por que um fóton, que não tem massa, tem energia? 
Fórmula de Bayes e Inteligência Artificial 
As sete constantes fundamentais da física 
Qual é a sensação de temperatura no espaço interestelar? 
Curvas de radiação do corpo negro: lei de Planck 
O princípio da equivalência, os efeitos gravitacionais são indistinguíveis da aceleração 
E=mc2: Os quatro conceitos fundamentais do universo revisitados 
Como pesar
o sol? 
Equação da queda livre dos corpos (1604) 
Equação de Coulomb (1785) 
Equação de Boltzmann sobre entropia (1877) 
As equações de Relatividade Restrita (1905) 
A equação da relatividade geral (1915) 
Equações da rotação planetária: entre momento cinético e equilíbrio gravitacional 
Equação da velocidade orbital de um planeta 
A equação
de Planck 
Equação de Schrödinger 
Como as três leis de Newton descrevem toda a mecânica clássica? 
Equações de Maxwell
A equação de Dirac 
Conservação da energia 
Equação da indução eletromagnética 
Por que as partículas elementares não têm massa? 
Diferença entre calor e temperatura