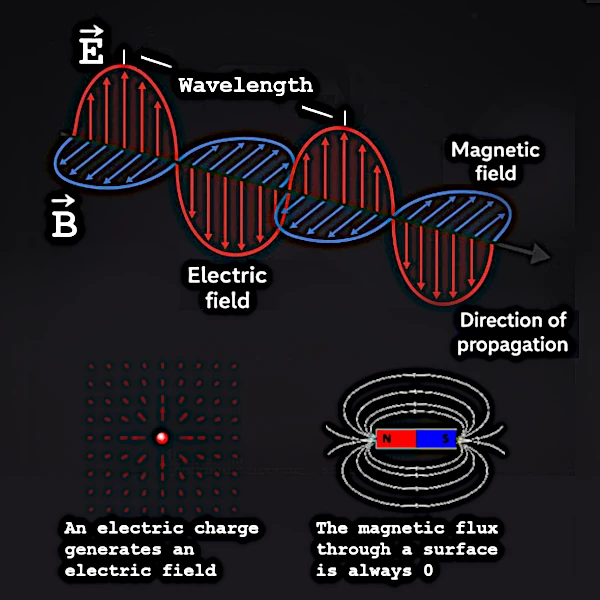
Todos los fenómenos electromagnéticos se reducen a un sistema de cuatro relaciones fundamentales: las ecuaciones de Maxwell. Estas ecuaciones por sí solas predicen todo sobre la dinámica de los campos eléctricos y magnéticos.
Las dos últimas ecuaciones son la clave del misterio del embalamiento. Un campo magnético variable en el tiempo (\( \partial \mathbf{B}/\partial t \)) crea un campo eléctrico rotativo. Simétricamente, un campo eléctrico variable (\( \partial \mathbf{E}/\partial t \)) crea un campo magnético rotativo. Es este acoplamiento dinámico el que se auto-mantiene a lo largo de su propagación.
Cuando James Clerk Maxwell (1831–1879) unificó las leyes de la electricidad y el magnetismo en el siglo XIX, descubrió un fenómeno sorprendente: una perturbación local de un campo eléctrico o magnético crea una onda que se propaga por sí sola en el vacío, sin necesidad de energía adicional.
Maxwell mostró que esta onda se desplaza a una velocidad finita, determinada por dos propiedades del vacío:
La fórmula \( c = \frac{1}{\sqrt{\mu_0 \varepsilon_0}} \) da esta velocidad.
Al combinar las leyes de Faraday y de Ampère-Maxwell, obtuvo una ecuación de onda. Al introducir los valores de μ₀ y ε₀, encontró: \( c \approx 300.000 \) km/s, ¡la velocidad de la luz!
En 1865, Maxwell concluyó que la luz es una onda electromagnética, al igual que las ondas de radio o las microondas. Un descubrimiento que revolucionó la física.
N.B.:
En la época de Maxwell (1865), la velocidad de la luz aún no se conocía con gran precisión. Las mediciones experimentales disponibles, realizadas notablemente por Armand Fizeau (1819-1896) y Albert Michelson (1852-1931), permitían estimar \( v \) con un margen de error significativo. El cálculo teórico de Maxwell dio, por lo tanto, un valor muy cercano a lo que más tarde sería confirmado, lo que constituyó una validación impresionante de su teoría.
Cuando Maxwell ensambló las leyes de la electricidad y el magnetismo, descubrió una estructura que se auto-mantiene, tan pronto como se perturba localmente un campo eléctrico o magnético. Este "embalamiento" es estable, sin amplificación, y no posee ninguna fuente de energía interna. El vacío transporta la onda sin alimentarla.
Este bucle dinámico entre \( \mathbf{B} \) y \( \mathbf{E} \), produce una estructura que se propaga en el vacío a velocidad finita.
El término \(\mu_0 \varepsilon_0\) de la cuarta ecuación fija la velocidad de la luz: \( c = \frac{1}{\sqrt{\mu_0 \varepsilon_0}}. \)
Al combinar matemáticamente las leyes de Faraday y de Ampère-Maxwell (tomando el rotacional de una y usando la otra), se elimina el acoplamiento para obtener una ecuación que describe cada campo por separado.
Para el campo eléctrico, se encuentra: \( \nabla^2 \mathbf{E} = \mu_0 \varepsilon_0 \frac{\partial^2 \mathbf{E}}{\partial t^2} \) Esta es la forma clásica de la ecuación de onda. El término \( \mu_0 \varepsilon_0 \) se encuentra frente a la derivada segunda temporal. En física matemática, la ecuación de onda estándar se escribe como \( \nabla^2 \psi = \frac{1}{v^2} \frac{\partial^2 \psi}{\partial t^2} \), donde \( v \) es la velocidad de propagación.
Por identificación inmediata: \( \frac{1}{v^2} = \mu_0 \varepsilon_0 \quad \Rightarrow \quad v = \frac{1}{\sqrt{\mu_0 \varepsilon_0}} \)
Maxwell calculó este valor con las constantes conocidas en su época:
El resultado es asombroso: \( v \approx 2.998 \times 10^{8} \, \text{m/s} \), ¡la velocidad de las ondas corresponde a la velocidad de la luz medida experimentalmente!
N.B.:
Esta demostración matemática supone el vacío, es decir, la ausencia de cargas y corrientes (\( \rho = 0, \, \mathbf{J} = 0 \)). El razonamiento consiste en tomar el rotacional de la ley de Faraday y utilizar la identidad vectorial \( \nabla \times (\nabla \times \mathbf{E}) = \nabla(\nabla \cdot \mathbf{E}) - \nabla^2 \mathbf{E} \), combinando con la ley de Gauss (\( \nabla \cdot \mathbf{E} = 0 \) en el vacío) y la ley de Ampère-Maxwell. Así se obtiene la misma ecuación de onda para el campo magnético \( \mathbf{B} \). Esta predicción teórica de James Clerk Maxwell (1831-1879) en 1865 fue confirmada experimentalmente por Heinrich Hertz (1857-1894) en 1887, cuando produjo las primeras ondas de radio.
Maxwell encontró que las ondas electromagnéticas se propagan a cierta velocidad en el vacío, pero la demostración de que esta es una velocidad límite aún no estaba establecida. Maxwell aún no conocía la relatividad. Por lo tanto, no tenía ninguna razón para pensar que era una velocidad límite universal. La noción de límite universal solo apareció con la relatividad especial, mucho después de Maxwell.
Fue solo con la relatividad especial (1905) de Albert Einstein (1879-1955) que la velocidad de la luz en el vacío \( c \) fue reconocida como la velocidad máxima a la que la información, la energía o cualquier interacción física puede propagarse. En otras palabras, \( c \) es un límite fundamental impuesto por la estructura del espacio-tiempo, y no solo una consecuencia de las ecuaciones de Maxwell.
Los fenómenos electromagnéticos obedecen a las ecuaciones de Maxwell y se resumen así:
Por lo tanto, la luz y todas las ondas electromagnéticas no son más que la manifestación de este fenómeno de auto-sostenimiento de los campos eléctricos y magnéticos en el vacío.
El Embalamiento Electromagnético: El Secreto de la Velocidad de la Luz 
Comprender el Efecto Fotoeléctrico: La Luz y los Electrones 
¿A qué distancia está el horizonte? 
¿Cómo Inyectan Electricidad los Paneles Solares en la Red? 
Dinámica del momento para explicar la propulsión de cohetes o medusas 
Distribución Energética de los Electrones en Átomos 
Principio de Incertidumbre de Heisenberg: Comprendiendo la Incertidumbre Cuántica 
Relación entre Energía, Potencia y Tiempo 
¿Por qué hay un límite para el frío, pero no para el calor? 
La Ley de la Caída de los Cuerpos de Galileo 
La Ley de los Gases Ideales 
Ecuación de Schrödinger y Estructura de los Átomos 
Teorema de Noether: la conservación de la energía surge de las simetrías 
Relación entre masa gravitacional y masa inercial y el principio de equivalencia 
La Tercera Ecuación Esencial en Física 
La segunda ecuación esencial en física 
La primera ecuación esencial en física 
La fuerza electromagnética o fuerza de Lorentz 
La energía solar recibida depende del ángulo de incidencia 
¿Por qué el mármol es más frío que la madera? 
¿Por qué un fotón que no tiene masa tiene energía? 
Fórmula de Bayes e inteligencia artificial 
Las siete constantes fundamentales de la física 
¿Qué temperatura se siente en el espacio interestelar? 
Curvas de radiación del cuerpo negro: ley de Planck 
El principio de equivalencia, los efectos gravitacionales son indistinguibles de la aceleración 
E=mc2: Los cuatro conceptos fundamentales del universo revisados 
¿Cómo pesar
el sol? 
Ecuación de la caída libre de cuerpos (1604) 
Ecuación de Coulomb (1785) 
Ecuación de Boltzmann sobre la entropía (1877) 
Las ecuaciones de la relatividad especial (1905) 
La ecuación de la relatividad general (1915) 
Ecuaciones de la rotación planetaria: entre momento cinético y equilibrio gravitacional 
Ecuación de la velocidad orbital de un planeta 
La
ecuación de Planck 
Ecuación de Schrödinger 
¿Cómo describen las tres leyes de Newton toda la mecánica clásica? 
Las ecuaciones
de Maxwell 
La ecuación de Dirac 
Conservación de la energía 
Ecuación de la inducción electromagnética 
¿Por qué las partículas elementales no tienen masa? 
Diferencia entre calor y temperatura