Le secret de la Vitesse de la lumière : l’emballement électromagnétique

Les 4 équations de Maxwell

L’ensemble des phénomènes électromagnétiques se ramène à un système de quatre relations fondamentales: les équations de Maxwell. À elles seules, ces équations prédisent tout sur la dynamique des champs électriques et magnétiques.

1. Loi de Gauss pour l’électricité: \(\nabla \cdot \mathbf{E} = \dfrac{\rho}{\varepsilon_0}\) (La divergence du champ électrique est proportionnelle à la densité de charge \(\rho\) → une charge électrique crée un champ électrique autour d’elle)
   
2. Loi de Gauss pour le magnétisme: \(\nabla \cdot \mathbf{B} = 0\) (Le flux magnétique net sur une surface fermée est nul → les lignes de champ magnétique forment des boucles fermées, il n’existe pas de monopôles magnétiques)
   
3. Loi de Faraday: \(\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}\) (Toute variation du champ magnétique dans le temps crée un champ électrique rotatif)
   
4. Loi d’Ampère–Maxwell: \(\nabla \times \mathbf{B} = \mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t}\) (Un champ électrique variable crée à son tour un champ magnétique)

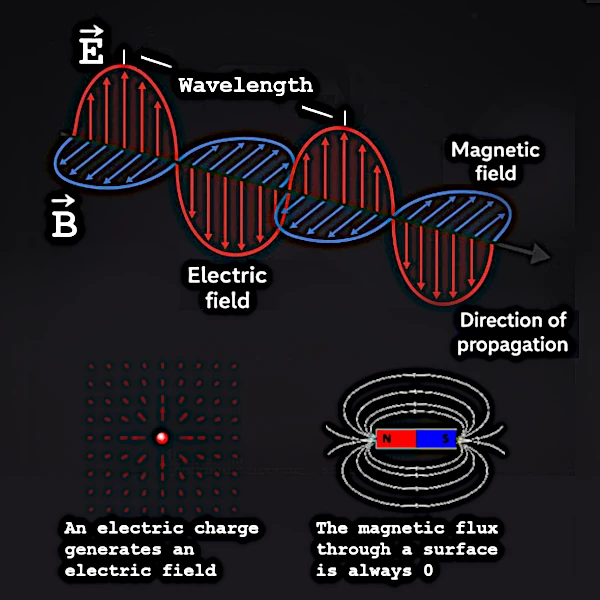
Les deux dernières équations sont la clé du mystère de l'emballement. Un champ magnétique variable dans le temps (\( \partial \mathbf{B}/\partial t \)) crée un champ électrique rotatif. Symétriquement, un champ électrique variable (\( \partial \mathbf{E}/\partial t \)) crée un champ magnétique rotatif. C'est ce couplage dynamique qui s’auto-entretient tout le long de leur propagation.

Maxwell et la découverte de la vitesse de la lumière

Lorsque James Clerk Maxwell (1831–1879) unifie les lois de l’électricité et du magnétisme au 19ᵉ siècle, il découvre un phénomène surprenant: une perturbation locale d’un champ électrique ou magnétique crée une onde qui se propage toute seule dans le vide, sans besoin d’énergie supplémentaire.

L'équation d'onde et la prédiction de la vitesse de la lumière

Maxwell montre que cette onde se déplace à une vitesse finie, déterminée par deux propriétés du vide:

La formule \( c = \frac{1}{\sqrt{\mu_0 \varepsilon_0}} \) donne cette vitesse.

• μ₀: capacité du vide à transporter un champ magnétique
• ε₀: capacité du vide à laisser passer un champ électrique

La lumière, une onde électromagnétique

En combinant les lois de Faraday et d’Ampère-Maxwell, il obtient une équation d’onde. En y injectant les valeurs de μ₀ et ε₀, il trouve: \( c \approx 300\,000 \) km/s, la vitesse de la lumière!

Conclusion de Maxwell

En 1865, Maxwell conclut que la lumière est une onde électromagnétique, tout comme les ondes radio ou les micro-ondes. Une découverte qui a révolutionné la physique.

N.B. :
À l’époque de Maxwell (1865), la vitesse de la lumière n’était pas encore connue avec une grande précision. Les mesures expérimentales disponibles, réalisées notamment par Armand Fizeau (1819-1896) et Albert Michelson (1852-1931), permettaient d’estimer \( v \) avec une marge d’erreur significative. Le calcul théorique de Maxwell donna donc une valeur très proche de ce qui serait confirmé plus tard, ce qui constitua une validation impressionnante de sa théorie.

Calcul de la vitesse de propagation des champs E et B

Lorsque Maxwell assemble les lois de l’électricité et du magnétisme, il découvre une structure qui s’auto-entretient, dès que l’on perturbe localement un champ électrique ou magnétique. Cet "emballement" est stable, sans amplification, et ne possède aucune source d’énergie interne. Le vide transporte l’onde sans la nourrir.

L'équation d'onde et la prédiction de la vitesse de la lumière

Cette boucle dynamique entre \( \mathbf{B} \) et \( \mathbf{E} \), produit une structure qui se propage dans le vide à vitesse finie.

Le terme \(\mu_0 \varepsilon_0\) de la quatrième équation fixe la vitesse de la lumière: \( c = \frac{1}{\sqrt{\mu_0 \varepsilon_0}}. \)

• \( \mu_0 \) = Constante de perméabilité du vide ou capacité du vide à transporter un champ magnétique
• \( \varepsilon_0 \) = Constante de permittivité électrique du vide ou capacité du vide à laisser “passer” un champ électrique

Obtention de l’équation d’onde électromagnétique

En combinant mathématiquement les lois de Faraday et d'Ampère-Maxwell (en prenant le rotationnel de l'une et en utilisant l'autre), on élimine le couplage pour obtenir une équation décrivant chaque champ seul.

Équation d’onde pour le champ électrique

Pour le champ électrique, on trouve: \( \nabla^2 \mathbf{E} = \mu_0 \varepsilon_0 \frac{\partial^2 \mathbf{E}}{\partial t^2} \) C'est la forme classique de l'équation d'onde. Le terme \( \mu_0 \varepsilon_0 \) se trouve devant la dérivée seconde temporelle. En physique mathématique, l'équation d'onde standard s'écrit \( \nabla^2 \psi = \frac{1}{v^2} \frac{\partial^2 \psi}{\partial t^2} \), où \( v \) est la vitesse de propagation.

Identification avec la vitesse d’une onde

Par identification immédiate: \( \frac{1}{v^2} = \mu_0 \varepsilon_0 \quad \Rightarrow \quad v = \frac{1}{\sqrt{\mu_0 \varepsilon_0}} \)

Résultat du calcul: La lumière est une onde électromagnétique

Maxwell calcule cette valeur avec les constantes connues de son époque:

• \( \mu_0 = 4\pi \times 10^{-7} \, \text{N} \cdot \text{A}^{-2} \)
• \( \varepsilon_0 \approx 8.854 \times 10^{-12} \, \text{C}^{2} \cdot \text{N}^{-1} \cdot \text{m}^{-2} \)

Le résultat est stupéfiant: \( v \approx 2.998 \times 10^{8} \, \text{m/s} \), la vitesse des ondes correspond à la vitesse de la lumière mesurée expérimentalement!

N.B. :
Cette démonstration mathématique suppose le vide, c’est-à-dire l’absence de charges et de courants (\( \rho = 0, \, \mathbf{J} = 0 \)). Le raisonnement consiste à prendre le rotationnel de la loi de Faraday et à utiliser l'identité vectorielle \( \nabla \times (\nabla \times \mathbf{E}) = \nabla(\nabla \cdot \mathbf{E}) - \nabla^2 \mathbf{E} \), en combinant avec la loi de Gauss (\( \nabla \cdot \mathbf{E} = 0 \) dans le vide) et la loi d'Ampère-Maxwell. On obtient ainsi la même équation d'onde pour le champ magnétique \( \mathbf{B} \). Cette prédiction théorique de James Clerk Maxwell (1831-1879) en 1865 fut confirmée expérimentalement par Heinrich Hertz (1857-1894) en 1887, lorsqu’il produisit les premières ondes radio (ondes électromagnétiques).

Limite des équations de Maxwell

Maxwell trouve que les ondes électromagnétiques se propagent à une certaine vitesse dans le vide, mais la démonstration que c'est une vitesse limite. Maxwell ne connaissait pas encore la relativité. Il n’avait donc aucune raison de penser que c’était une vitesse limite universelle. La notion de limite universelle n’est apparue que avec la relativité restreinte, bien après Maxwell.

Ce n’est qu’avec la relativité restreinte (1905) d’Albert Einstein (1879-1955) que la vitesse de la lumière dans le vide \( c \) a été reconnue comme **vitesse maximale à laquelle l’information, l’énergie ou toute interaction physique peut se propager**. Autrement dit, \( c \) est une **limite fondamentale imposée par la structure de l’espace-temps**, et non une simple conséquence des équations de Maxwell.

Ce qu’il faut retenir

Les phénomènes électromagnétiques obéissent aux équations de Maxwell et se résument ainsi :

• Une charge électrique (charge électrique) crée un champ électrique autour d’elle.
• Un champ magnétique variable dans le temps engendre un champ électrique.
• Un champ électrique variable dans le temps crée à son tour un champ magnétique.
• Ces deux champs s’autoentretiennent, se propageant dans l’espace sous forme d’ondes électromagnétiques à la vitesse de la lumière.

Ainsi, la lumière et toutes les ondes électromagnétiques ne sont rien d’autre que la manifestation de ce phénomène d’auto-entretien des champs électriques et magnétiques dans le vide.