Équations de la rotation planétaire : entre moment cinétique et équilibre gravitationnel

Le mouvement de rotation planétaire

Exemples de vitesses de rotation dans le Système solaire

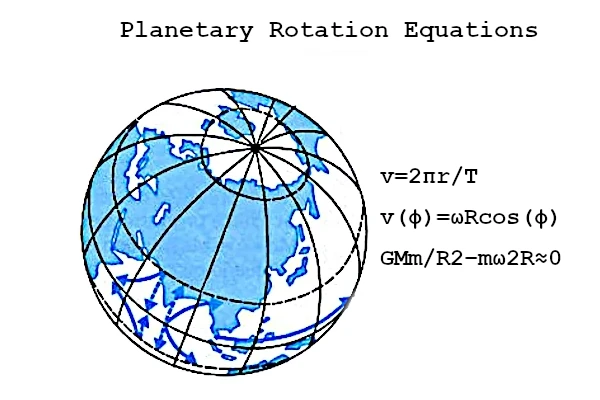
Pour illustrer cette équation, prenons quelques exemples caractéristiques du Système solaire. La Terre, dont le rayon moyen est de \(r = 6\,371 \text{ km}\) et la période de rotation \(T = 24 \text{ h}\), présente une vitesse équatoriale d’environ \(v = \frac{2\pi r}{T} ≈ 1\,670 \text{ km/h}\).
La planète Mars, plus petite avec un rayon de \(r = 3\,389 \text{ km}\) et une période de rotation de \(T = 24 \text{ h } 36 \text{ min}\), tourne plus lentement, sa vitesse équatoriale atteignant environ \(868 \text{ km/h}\) à l’équateur martien.

Influence du rayon et de la période de rotation

Cette relation montre que la vitesse de rotation dépend directement du rayon de la planète et de la durée de sa journée sidérale. Une planète plus grande ou tournant plus rapidement possède une vitesse de rotation plus élevée à l’équateur. Inversement, une planète compacte ou lente aura une vitesse linéaire plus faible.

Variation de la vitesse avec la latitude

Enfin, il est important de noter que cette vitesse n’est valable que pour l’équateur. À mesure que l’on s’approche des pôles, la distance à l’axe de rotation diminue et la vitesse de rotation devient \(v(\phi) = \omega R \cos(\phi)\), où \(\phi\) est la latitude. Ainsi, bien que la période de rotation reste identique pour tous les points du globe (24 h pour la Terre), la vitesse linéaire décroît continûment jusqu’à devenir nulle aux pôles.

Le rôle du moment cinétique

Le mouvement de rotation d’une planète autour de son axe est gouverné par son moment cinétique \(L\), défini par la relation fondamentale : \((L = I \omega)\) où \(I\) est le moment d’inertie et \(\omega\) la vitesse angulaire. Cette équation exprime la distribution de la masse autour de l’axe et la rapidité de rotation. Une planète en équilibre conserve son moment cinétique tant qu’aucune force externe ne vient exercer de couple sur elle.

Variations et implications de la vitesse de rotation

La vitesse nulle aux pôles

Aux pôles Nord et Sud, la vitesse de rotation est en réalité nulle, car ces points coïncident avec l’axe de rotation de la Terre. Ainsi, bien que la Terre tourne sur elle-même, les pôles restent immobiles par rapport à cet axe : ils ne décrivent aucun cercle, contrairement aux points situés à des latitudes plus basses.

L’évolution de la rotation terrestre au cours du temps

Il y a environ 600 millions d’années, la journée terrestre durait environ 22 heures. Cela indique que la Terre tournait plus rapidement qu’aujourd’hui. Le ralentissement progressif de la rotation est dû à l’interaction gravitationnelle avec la Lune (un phénomène connu sous le nom de freinage de marée).

Les limites de l’équation \(v = \frac{2\pi r}{T}\)

Cette relation simple n’est pas universelle. Elle s’applique bien aux corps solides en rotation uniforme, comme les planètes telluriques, mais pas aux étoiles, dont la structure fluide engendre une rotation différentielle. Autrement dit, la période de rotation dépend de la latitude : les régions équatoriales tournent plus vite que les zones polaires.

Exemple : la rotation différentielle du Soleil

Dans le cas du Soleil, la période de rotation varie d’environ 25 jours à l’équateur à 34 jours aux pôles. Cette différence reflète la nature plasmique du Soleil, où les couches ne sont pas rigides. Sa vitesse de rotation équatoriale atteint environ 2 km/s.

Intérêt physique de la relation \(v = \frac{2\pi r}{T}\)

La connaissance de la vitesse de rotation d’un astre est essentielle pour comprendre ses caractéristiques physiques et ses processus dynamiques. Elle est directement liée à la durée de la journée sidérale et fournit des indices sur l’évolution interne et l’histoire de la planète.

Par exemple, sur Jupiter, la rotation extrêmement rapide (moins de 10 heures) engendre d’immenses cellules de convection et des tempêtes cycloniques géantes, dont la plus célèbre est la Grande Tache Rouge.

Le lien entre gravitation et rotation

La rotation planétaire résulte d’un équilibre entre l’attraction gravitationnelle et la force centrifuge. L’équilibre dynamique est atteint lorsque la force centrifuge à la surface compense partiellement la gravitation : \((\frac{G M m}{R^2} - m \omega^2 R \approx 0)\) où \(G\) est la constante gravitationnelle, \(M\) la masse de la planète, \(m\) la masse d’un corps en surface, et \(R\) le rayon planétaire. Cette relation montre que la rotation rapide d’une planète tend à diminuer la pesanteur apparente à l’équateur.

Conséquences dynamiques et stabilité

Les planètes ne conservent pas éternellement leur vitesse de rotation. Sous l’effet des forces de marée, leur moment cinétique peut se transférer vers leur satellite ou vers leur orbite. Ainsi, la Terre ralentit progressivement, et la Lune s’éloigne d’environ 3,8 cm par an. Cette dissipation d’énergie tend vers un état de rotation synchrone, comme celle observée entre la Lune et la Terre.

La stabilité rotationnelle dépend aussi de la distribution de masse interne. Les planètes fluides comme Jupiter ou Saturne présentent un fort aplatissement dû à leur grande vitesse angulaire \((\omega)\), tandis que les planètes rocheuses, plus rigides, résistent davantage à cette déformation.

Origine du moment cinétique planétaire

Lors de la formation du disque protoplanétaire, les collisions et les effondrements locaux ont imposé un mouvement préférentiel de rotation. Le moment cinétique global s’est distribué entre le Soleil, les planètes et leurs satellites. Cette répartition, déjà analysée par Isaac Newton (1643-1727) et formalisée plus tard par Laplace (1749-1827), explique la rotation quasi uniforme des corps planétaires autour d’un même plan écliptique.

Équations fondamentales de la rotation

On définit la vitesse linéaire d’un point à la surface par : \((v = \omega R)\) et la période de rotation \(T\) par : \((\omega = \frac{2\pi}{T})\)
Ces équations relient les grandeurs observables et permettent de calculer la durée du jour planétaire. Par exemple, Jupiter, avec un rayon \(R = 71\,492 \text{ km}\) et \(T = 9,93 \text{ h}\), possède une vitesse équatoriale \(v ≈ 12,6 \text{ km/s}\), bien supérieure à celle de la Terre \((0,465 \text{ km/s})\).

N.B. :
Les effets gyroscopiques d’une planète en rotation expliquent la précession des équinoxes et les variations lentes de l’inclinaison de l’axe. Ces phénomènes influencent directement le climat sur des échelles de temps de plusieurs milliers d’années (cycles de Milankovitch).

Source : NASA Planetary Fact Sheet, Astronoo.