Image description: Imagine pushing a box across a smooth floor. The harder you push (the greater the force F), the more the box will accelerate (the greater the acceleration a). If the box is very heavy (mass m is large), it will accelerate less for the same applied force.
The most fundamental and universally recognized equation is Newton's second law (1643-1727).
Note: Newton's first law, also known as the principle of inertia, is a fundamental concept in physics that describes the behavior of an object when no net force is acting on it. There is no single equation for Newton's first law.
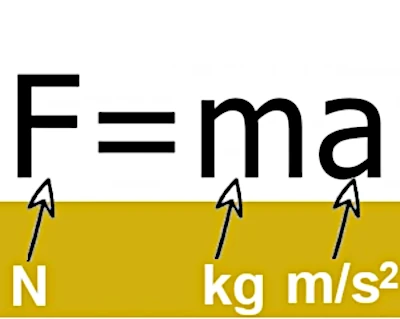
F = ma is a fundamental equation in physics, more specifically in classical mechanics. It expresses a relationship between three essential physical quantities:
• $ \vec{F} $ is the force applied to an object, expressed in newtons (N),
• m is the mass of the object, expressed in kilograms (kg),
• a is the acceleration of the object, expressed in meters per second squared (m/s²).
This equation describes the relationship between the force applied to an object, the mass of the object, and the resulting acceleration. It is essential because it establishes the link between classical mechanics and the movement of bodies. Furthermore, it serves as the basis for many other equations and concepts in physics.
It can be seen as one of the starting equations for understanding the dynamics of systems and introduces fundamental concepts such as force, mass, and acceleration.
The concept of force is one of the fundamental notions in classical physics, particularly in the context of Newtonian mechanics. It is defined as any interaction that, when exerted on an object, modifies the state of motion of that object. The force can cause an acceleration, a change of direction, or a deformation of the object in question.
In the formalism of classical mechanics, a force $ \vec{F} $ is a vector quantity, that is, a quantity that has a direction, a sense, and an intensity.
Force is proportional to acceleration: the greater the applied force, the greater the acceleration of the object will be.
Mass resists acceleration: the greater the mass of an object, the harder it will be to move it or change its speed (i.e., to accelerate it).
In other words, F = ma tells us that to alter the motion of an object (to set it in motion, stop it, change its direction, or speed it up), a force must be applied.
It is important to note that F = ma is a simplification. It is valid within the framework of classical mechanics and for speeds much lower than the speed of light. For very high speeds, Einstein's theory of relativity must be used. Additionally, this equation does not account for certain forces such as frictional forces.
The Third Essential Equation in Physics
The Second Essential Equation in Physics
The electromagnetic force or Lorentz force
The solar energy received depends on the angle of incidence
Why is marble colder than wood?
Planck's wall theory