Image description: Electrons occupy specific orbitals, defined by quantum numbers, and their energy depends on their position in the atom. Image source: Astronoo.
Electron energy in a polyelectronic atom is a central concept in quantum mechanics. Unlike the hydrogen atom, which has only one electron, polyelectronic atoms contain multiple electrons interacting with each other and the nucleus. These complex interactions make calculating electron energy more difficult but essential for understanding the chemical and physical properties of elements.
Electron energy helps understand atomic structure and the properties of elements. The Schrödinger equation, atomic orbitals, and shielding effects play a key role in determining energy levels and electron configuration.
The energy of electrons in an atom is described by the Schrödinger equation, a fundamental equation in quantum mechanics. For a polyelectronic atom, the Schrödinger equation is written as:
\[ \hat{H} \Psi = E \Psi \]
where \(\hat{H}\) is the Hamiltonian operator, \(\Psi\) is the electron's wave function, and \(E\) is the energy associated with this state. The Hamiltonian includes kinetic energy and potential energy terms, the latter accounting for interactions between electrons and the nucleus, as well as interactions between the electrons themselves.
Solving this equation gives the atomic orbitals, which describe the spatial distribution of electrons around the nucleus. Each orbital is characterized by three quantum numbers: the principal quantum number \(n\), the azimuthal quantum number \(l\), and the magnetic quantum number \(m\). These quantum numbers determine the energy and shape of the orbitals.
In a polyelectronic atom, electrons are distributed across different energy levels, defined by the principal quantum number \(n\). Electrons first fill the lowest energy levels, according to the Pauli Exclusion Principle and Hund's Rule. The electron configuration of an atom describes the distribution of electrons in the orbitals.
N.B.: The Pauli Exclusion Principle forbids two electrons from having the same four quantum numbers (n, l, ml, ms), while Hund's Rule predicts that electrons occupy degenerate orbitals with parallel spins before pairing.
Carbon (\(Z = 6\)) has 6 electrons. These electrons are distributed in atomic orbitals according to the rules of quantum mechanics. The electron configuration of carbon is:
\[ 1s^2 \, 2s^2 \, 2p^2 \]
This means:
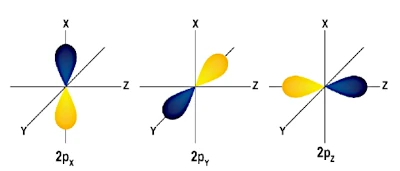
The \(p\) orbitals come in three types, corresponding to three different spatial orientations:
The \(p\) orbitals have "dumbbell" shapes (or lobes) oriented along the \(x\), \(y\), and \(z\) axes. These three orbitals are orthogonal to each other, meaning they occupy distinct regions of space.
These three \(p\) orbitals are degenerate, meaning they have the same energy. In the case of carbon, the 2 remaining electrons are distributed in these \(2p\) orbitals. According to Hund's Rule, electrons first occupy distinct \(p\) orbitals with parallel spins before pairing. Thus, for carbon:
In the case of carbon, the 2 electrons in the \(2p\) orbitals occupy two of the three available orbitals (\(p_x\) and \(p_y\)), leaving the third (\(p_z\)) empty. This shows that electrons do not distribute uniformly in space but occupy specific regions defined by the atomic orbitals. This distribution is essential for understanding the chemical properties of carbon, particularly its ability to form covalent bonds in specific directions.
In a polyelectronic atom, inner electrons partially "shield" the positive charge of the nucleus for outer electrons. This shielding effect reduces the effective attraction of the nucleus on outer electrons, influencing their energy. The effective energy felt by an electron can be approximated by the formula:
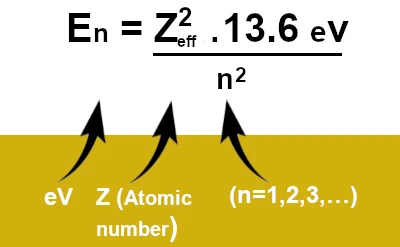
\[E_n = -\frac{Z_{\text{eff}}^2 \cdot 13.6 \, \text{eV}}{n^2}\]
where \(Z_{\text{eff}}\) is the effective nuclear charge, accounting for the shielding effect, and \(n\) is the principal quantum number. This formula shows that the energy of electrons depends on their average distance from the nucleus and the effective charge felt.
The energy of electrons in the \(2p\) orbitals can be estimated using the hydrogen-like atom model, although this model is a simplification for polyelectronic atoms like carbon. The energy \(E_n\) of an electron in an orbital with principal quantum number \(n\) is given by the formula:
\[E_n = -\frac{Z_{\text{eff}}^2 \cdot R_H}{n^2}\]
where:
For the electrons in the \(2p\) shell of carbon, \(n = 2\). The effective nuclear charge \(Z_{\text{eff}}\) for the \(2p\) electrons of carbon is approximately \(3.14\) (this value may vary depending on the calculation model). Thus, the energy of the electrons in the \(2p\) orbitals is:
\[E_{2p} = -\frac{(3.14)^2 \cdot 13.6 \, \text{eV}}{2^2} \approx -30.6 \, \text{eV}\]
This energy is higher than that of the electrons in the \(1s\) (E1s≈−489.6eV) and \(2s\) (E2s≈−35.1eV) orbitals, explaining why the \(2p\) electrons are less tightly bound to the nucleus.
In the case of carbon, the 2 electrons in the \(2p\) orbitals occupy two of the three available orbitals (\(p_x\) and \(p_y\)), leaving the third (\(p_z\)) empty. This shows that electrons do not distribute uniformly in space but occupy specific regions defined by the atomic orbitals. This distribution is essential for understanding the chemical properties of carbon, particularly its ability to form covalent bonds in specific directions.
The energy of electrons in an atom is measured relative to a reference state, which is usually the energy of a free electron (i.e., an electron no longer bound to the nucleus). By convention, the energy of a free electron is defined as 0 eV. A negative energy means the electron is bound to the nucleus. The more negative the energy, the more tightly the electron is bound to the nucleus. Although −30.6eV is numerically larger than −489.6eV, it is less negative. This means the energy of the electron in the 2p orbital is closer to zero than that of the electron in the 1s orbital.
Heisenberg's Uncertainty Principle: Understanding Quantum Uncertainty 
Relation between Energy, Power, and Time 
Why is there a limit to cold, but not to heat? 
Galileo's Law of Falling Bodies 
The Ideal Gas Law 
Schrödinger Equation and Atomic Structure 
Noether's Theorem: conservation of energy follows from symmetries 
Relationship
between gravitational mass and inertial mass and the equivalence principle 
The Third Essential Equation
in Physics 
The Second Essential Equation
in Physics 
The first essential equation
in physics 
The electromagnetic force or Lorentz force 
The solar energy received depends on
the angle of incidence 
Why is marble colder
than wood? 
Planck's wall theory