The three laws of Isaac Newton (1643-1727) form the conceptual and mathematical basis of classical mechanics. They express, in the form of equations, the fundamental relationships between the concepts of force, mass, and acceleration. These laws, published in the *Philosophiæ Naturalis Principia Mathematica* in 1687, made it possible to understand and predict the motion of terrestrial and celestial objects with remarkable precision.
The first law, known as the principle of inertia, states that a body remains at rest or in uniform rectilinear motion unless acted upon by a net force. It can be expressed by the equation: \(\sum \vec{F} = 0 \Rightarrow \vec{v} = \text{constant}\). This law asserts the existence of an inertial reference frame in which objects experience no net acceleration.
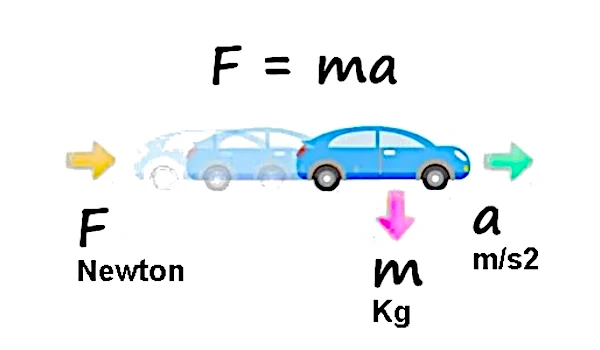
The second law quantitatively relates the applied force to the change in velocity. It is written as: \(\sum \vec{F} = m \vec{a}\), where \(m\) is the mass of the body and \(\vec{a}\) is its acceleration. This equation expresses the core of Newtonian mechanics: any change in motion is caused by a force, and the proportionality depends on the mass. In a non-inertial reference frame, fictitious forces must be introduced to restore this relationship.
The third law states that for every action exerted by body A on body B, there is an equal and opposite reaction exerted by B on A. Mathematically, this is written as: \(\vec{F}_{AB} = -\vec{F}_{BA}\). This principle of action-reaction expresses the symmetry of interactions and the conservation of momentum in an isolated system. Thus, when a cannon fires a cannonball, the force that accelerates the projectile simultaneously causes the cannon to recoil.
Together, these three laws make it possible to describe any mechanical situation on a human or planetary scale: falls, oscillations, orbits, or collisions. They introduce a clear causality between forces and motions, and make mass a universal constant linking mechanical energy to interactions. This framework dominated physics until the emergence of special relativity, formulated by Albert Einstein (1879-1955) in 1905, which shows that Newton's laws are only an approximation valid when the speed is much less than that of light \(v \ll c\).
N.B.:
Newton's laws cease to be exact at relativistic speeds or at the subatomic particle scale. They are then replaced by the laws of relativity and quantum mechanics. However, in 99.9% of practical cases, they remain perfectly valid and are used in all engineering disciplines.
| Law | Mathematical Formulation | Physical Principle | Comment |
|---|---|---|---|
| 1st Law: Inertia | \(\sum \vec{F} = 0 \Rightarrow \vec{v} = \text{const.}\) | Conservation of motion without force | Defines inertial reference frames |
| 2nd Law: Dynamics | \(\sum \vec{F} = m \vec{a}\) | Force proportional to acceleration | Basis for mechanical calculations and trajectories |
| 3rd Law: Action-Reaction | \(\vec{F}_{AB} = -\vec{F}_{BA}\) | Symmetry of mechanical interactions | Conservation of momentum |
Source: Stanford Encyclopedia of Philosophy – Laws of Motion and Physics.info – Newton’s Laws.