Primeira Medição da Distância Terra-Sol

Tamanho Relativo do Sistema Solar

No início do século XVII, os cientistas não tinham ideia das dimensões do sistema solar.

Graças às leis de Johannes Kepler (1571−1630) conhecemos as distâncias relativas dos cinco planetas da época em relação ao Sol. Em outras palavras, conhecemos as distâncias em uma unidade desconhecida, a distância Terra-Sol, mas não conhecemos a distância Terra-Sol em km.

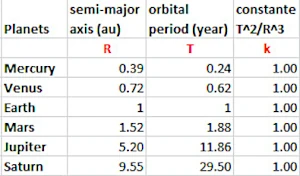
A 3ª lei de Johannes Kepler formulada em 1618 mostra a relação entre o semi-eixo maior da órbita de um planeta e seu período de rotação ao redor do Sol (tabela à direita). O cubo do semi-eixo maior é igual ao quadrado do período de rotação (T2 / R3 = k), o que posiciona a órbita de Mercúrio a 0.39 ua (unidade astronômica criada muito mais tarde em 1958) e a de Saturno a 9.55 unidades astronômicas do Sol.

A medição de uma única distância (planeta-Sol) dará a escala de todo o sistema e, portanto, a distância Terra-Sol em km tão esperada pelos astrônomos. Em 1687, Isaac Newton descobriu a lei da gravitação, que lhe permitiu explicar as três leis de Kepler.

Medição da Distância Terra-Marte

Tão paradoxal quanto possa parecer, foi medindo a distância Terra-Marte que os astrônomos e matemáticos do século XVII puderam ter uma ideia das dimensões do sistema solar. Naquela época, a observação resumia-se principalmente à medição dos ângulos dos objetos celestes vistos da Terra. Em seguida, os cálculos de trigonometria dão as distâncias.

Como foi calculada a distância Terra-Marte pela primeira vez?

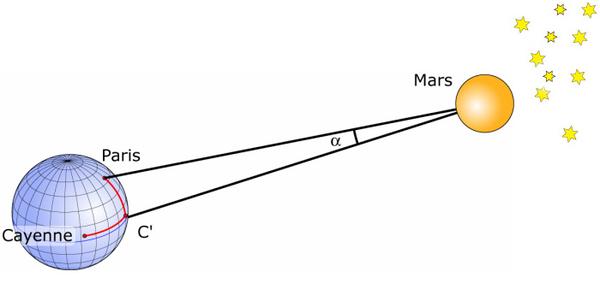
Em setembro de 1672, Jean-Dominique Cassini (1625−1712), Jean Picard, conhecido como o abade Picard (1620−1682), e Jean Richer (1630−1696) mediram a paralaxe horizontal de Marte quando este planeta passava mais perto da Terra (Marte está então, visto da Terra, oposto ao Sol). Para realizar esta medição, é necessário observar as posições de Marte em relação às estrelas muito mais distantes a partir de dois pontos muito distantes.

Cassini de Paris e Richer de Caiena medem a paralaxe de Marte. Esta medição relacionada à base formada pelo raio equatorial da Terra dá uma paralaxe horizontal de p=24" ⇒ Terra-Marte = 54,746,000 km. Para determinar a paralaxe de Marte a partir das observações feitas de Paris e Caiena, é necessário conhecer com a máxima precisão a diferença entre as latitudes e a diferença entre as longitudes de Paris e Caiena.

A latitude é fácil de medir, mas a longitude é muito mais difícil na época.

Cassini especifica, no entanto, que mediu a longitude por vários métodos para obter uma média:

• A observação de um eclipse cujas diferentes fases são anotadas em horas do meridiano de Paris, nos registros astronômicos.
• A observação dos eclipses dos satélites galileanos de Júpiter, que ocorrem várias vezes por dia.
• A observação das alturas meridianas do Sol.

O conjunto dá uma média de 3 h 39 min ±10 min. Richer e Cassini observam, portanto, o planeta Marte durante o mês de setembro de 1672. Marte passará perto de uma estrela de Aquário (Ψ Aquarii). Na imagem, o ponto C' corresponde à latitude de C (Caiena) e à longitude de P (Paris). Cassini usa duas observações simultâneas de Marte, uma de P, a outra de C'. O ângulo Paris Caiena a partir de Marte é o ângulo α=14". Mas a paralaxe de Marte é o ângulo sob o qual Marte vê o raio da Terra. O cálculo de proporcionalidade entre o ângulo Paris Caiena e a paralaxe de Marte dá 24" ± 5"

Uma vez conhecida a paralaxe de Marte, a trigonometria permite obter a distância Terra-Marte (D) em função do raio (R) da Terra:
D = R×3600/24×180/π ou 8600 R
D = 8600 * 6371 = 54,790,600 km

Cálculo da Distância Terra-Sol

Assim que a distância Terra-Marte foi conhecida, a distância Terra-Sol pôde ser calculada graças à terceira lei de Kepler.

Cassini sabia que Marte estava a 0.38 ua = 3/8 ua. Terra-Sol = 8/3 x 8600 R = 23000 R ±5000 raios terrestres. Cassini nos dá o valor do raio terrestre em léguas: R = 1500 léguas.

Na época, havia um grande número de definições de légua dependendo das regiões. Suponhamos que o raio terrestre seja dado na légua do abade Picard que a partir de 1671 é igual a 3707 metros. R = 1500 x 3.707 = 5560.5 km daí: Terra-Sol = 127,891,500 km a ±27,802,500 km

Este resultado notável constitui a primeira medição da distância Terra-Sol. Graças à terceira lei de Kepler, esta distância dará a escala de todo o sistema solar T2/R3=k.

Cálculo de Distâncias a Partir das Órbitas da Terra e Marte

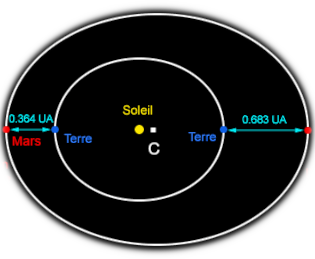
C = Centro da elipse que representa a órbita de Marte
CM_marte = Semi-eixo maior da órbita de Marte
Excentricidade da órbita de Marte = CS_sol / CM_marte = 0.093
CM_marte = CS_sol + S_solT_terra + T_terraM_marte
CM_marte = T_terraM_marte + S_solT_terra / 1-CS_sol
T_terraM_marte = 54,790,600 km
PT_terra (período da Terra) = 1 ano (365 dias)
PM_marte (período de Marte) = 1.88 anos (686 dias)
T_terraS_sol = T_terraM_marte / 1-CS_sol(PM_marte/PT_terra)2/3 -1
1-CS_sol(PM_marte/PT_terra)2/3 -1 = 0.38 ou 3/8 ⇒ T_terraS_sol = 54,790,600 x 8/3 = 150,000,000 km