地球と太陽の距離を初めて測定

太陽系の相対的な大きさ

17世紀初頭、科学者たちは太陽系の大きさについてまったく知りませんでした。

法律のおかげで、ヨハネス・ケプラー(1571−1630) 我々は、太陽に対する当時の 5 つの惑星の相対距離を知っています。言い換えれば、私たちは地球と太陽の距離という未知の単位での距離は知っていますが、地球と太陽の距離をキロメートル単位で知ることはできません。

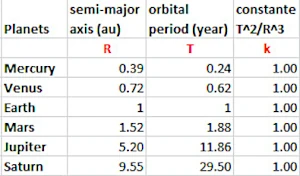
1618 年に定式化されたヨハネス ケプラーの第 3 法則は、惑星の軌道の長半径と太陽の周りの回転周期との関係を示しています (反対側の表)。長半径の 3 乗は自転周期の 2 乗 (T2 / R3 = k) に等しく、これにより水星の軌道は 0.39 天文単位 (1958 年にずっと後に作成された天文単位) に位置し、土星の軌道は太陽から 9.55 天文単位に位置します。

単一の距離 (惑星 - 太陽) の測定により、システム全体のスケールが得られ、したがって天文学者が待ち望んでいた地球と太陽の距離 (km) が得られます。 1687 年、アイザック ニュートンは重力の法則を発見し、これによりケプラーの 3 つ法則を説明できました。

地球と火星の距離を測定する

逆説的に見えるかもしれませんが、17 世紀の天文学者や数学者は、地球と火星の距離を測定することによって、太陽系の寸法についてのアイデアを得ることができました。当時の観測は、地球から見た天体の角度を測定することが主でした。次に、距離を求めるのは三角法の計算です。

地球と火星の距離はどのようにして初めて計算されたのでしょうか?

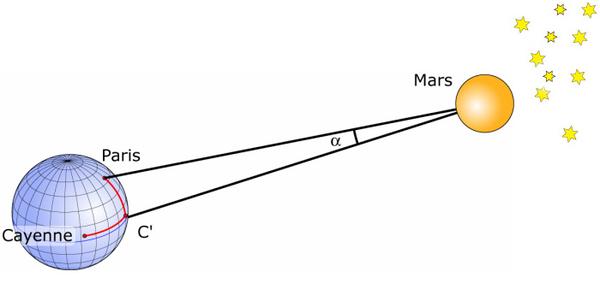
1672 年 9 月、ジャン＝ドミニク・カッシーニ (1625 − 1712 年)、アベ・ピカール (1620 − 1682 年) として知られるジャン・ピカール、およびジャン・リシェ (1630 − 1696 年) は、火星が地球に最接近したときの水平視差を測定しました (当時、地球から見た火星は太陽の反対側にありました)。この測定を実行するには、非常に離れた 2 つの点から、はるかに離れた星との関係で火星の位置を観測する必要があります。

パリのカッシーニとカイエンのリチャーは火星の視差を測定します。地球の赤道半径によって形成される基底を参照したこの測定により、p=24" ⇒ 地球-火星 = 54,746,000 km の水平視差が得られます。パリとカイエンヌからの観測から火星の視差を決定するには、パリとカイエンヌの緯度の差と経度の差を最大限の精度で知る必要があります。

当時、緯度を測定するのは簡単ですが、経度を測定するのははるかに困難でした。

ただし、カッシーニは、平均を得るためにいくつかの方法で経度を測定したと述べています。

• 天文コレクションで、パリ子午線の時間ごとに異なる位相が特定される日食の観察。
• 1日に数回起こる木星のガリレオ衛星食の観測。
• 太陽の子午線高さの観測。

すべて合わせると、平均は 3 時間 39 分 ±10 分になります。したがって、リチャーとカッシーニは、1672 年 9 月に火星を観察しました。火星は、みずがめ座の恒星 (Ψ Aquarii) の近くを通過します。画像上の点 C' は、C (カイエンヌ) の緯度、P (パリ) の経度に対応します。カッシーニは、火星の 2 つの同時観測を使用します。1 つは P から、もう 1 つは C’ からです。火星からのパリ カイエン角は、角度 α=14 インチです。ただし、火星の視差は、火星から地球の半径を見る角度です。パリ カイエン角と火星の視差との比例を計算すると、24 インチ ± 5 インチとなります。

火星の視差がわかれば、三角法を使用して地球と火星の距離 (D) を地球の半径 (R) の関数として求めることができます。
D = R×3600/24×180/π または 8600 R
D = 8600 * 6371 = 54,790,600 km

地球と太陽の距離の計算

地球と火星の距離がわかるとすぐに、地球と太陽の距離はケプラーの第 3 法則を使用して計算できるようになりました。

カッシーニは、火星が 0.38 天文単位 = 3/8 天文単位にあることを知っていました。地球-太陽 = 8/3 x 8600 R = 23000 R ±5000 地球半径。カッシーニは、地球の半径の値をリーグ単位で示します: R = 1500 リーグ。

当時、リーグの定義は地域によって多数ありました。地球の半径がアベ ピカール リーグで与えられ、1671 年から 3707 メートルに等しいと仮定します。 R = 1500 x 3.707 = 5560.5 km ここから: 地球-太陽 = 127,891,500 km (±27,802,500 km)

この注目すべき結果は、地球と太陽の距離を初めて測定したものです。ケプラーの第 3 法則のおかげで、この距離は次のようになります。太陽系全体の規模T2/R3=k。

地球と火星の軌道からの距離を計算する

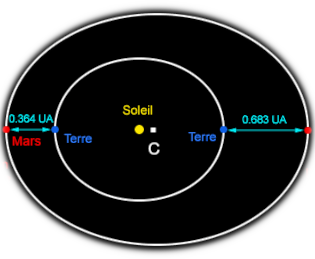
C = 火星の軌道を表す楕円の中心
CM_行進= 火星の軌道の長半径
火星の軌道離心率 = CS_太陽/CM_行進 = 0.093
CM_行進=CS_太陽+S_太陽T_地球+T_地球M_行進
CM_行進=T_地球M_行進+S_太陽T_地球/1-CS_太陽
T_地球M_行進= 54,790,600 km
P.T._地球(地球周期) = 1年(365日)
午後_行進(火星の周期) = 1.88 年 (686 日)
T_地球S_太陽=T_地球M_行進/1-CS_太陽(午後_行進/PT_地球)2/3 -1
1-CS_太陽(午後_行進/PT_地球)2/3 -1 = 0.38 または 3/8 ⇒ T_地球S_太陽= 54,790,600 x 8/3 = 150,000,000 km