Die Geometrie der Zeit: Erforschung der vierten Dimension des Universums

Konzept der Zeit

Seit Beginn des 20. Jahrhunderts^eJahrhundert, die Vorstellung vonZeithat aufgehört, ein einfacher, immer vorhandener universeller Parameter zu sein, sondern ist zu einer Dimension geworden, die in die Struktur des Universums selbst integriert ist. Die Theorie der speziellen Relativitätstheorie, formuliert 1905 vonAlbert Einstein(1879-1955) zeigte, dass die gemessene Dauer von der relativen Bewegung des Beobachters abhängt. Im Jahr 1915 führte die Allgemeine Relativitätstheorie die Krümmung des einRaumzeit (vierdimensionale Struktur, die Raum und Zeit verbindet)unter der Wirkung von Masse und Energie.

Zeit und Raum vereint: eine geometrische Einheit

L'Raumzeit (satz aus drei räumlichen Dimensionen und Zeit, die eine vierdimensionale Mannigfaltigkeit bilden)kann als vierdimensionale Mannigfaltigkeit beschrieben werden, in der Ereignisse die Koordinaten \((x, y, z, ct)\) haben. Die Minkowski-Metrik, die das formalisiertRaum-Zeit-Intervallder Speziellen Relativitätstheorie wurde 1908 von formuliertHermann Minkowski (1864-1909).
Es definiert das invariante Intervall: $$ \boxed{\color{blue}{\displaystyle s^2}} = (ct)^2 - x^2 - y^2 - z^2 $$
Diese Beziehung zeigt, dass Zeit und Raum eng miteinander verbunden sind und dass die Geometrie der Zeit hängt von der Geschwindigkeit des Beobachters sowie der Gravitation ab.

Warum c und t in Raum-Zeit-Koordinaten in Beziehung setzen?

Wir schreiben die Koordinaten eines Ereignisses oft als(x,y,z,ct)statt (x, y, z, t), also die zeitliche Komponentecthat die gleiche Dimension (Länge) wie die Raumkoordinaten.
Ausgabe:x, y und z werden in Metern ausgedrückt, während ���� in Sekunden ausgedrückt wird → Es ist nicht möglich, sie direkt in einem Standard oder einer Entfernung zu addieren.
Die Lösung:Multiplizieren Sie ���� mit ���� (Lichtgeschwindigkeit), die die Einheit m/s hat: ��������[m]. CT wird also in Metern angegeben, wie x,y,z. Diese Homogenität macht das Minkowski-Intervall, \( \boldsymbol{s^2} = (ct)^2 - x^2 - y^2 - z^2 \), kompakter und ermöglicht die Darstellung von Raum und Zeit im gleichen vierdimensionalen geometrischen Rahmen.

Die Minkowski-Metrik und Raumzeit

Art des Raum-Zeit-Intervalls

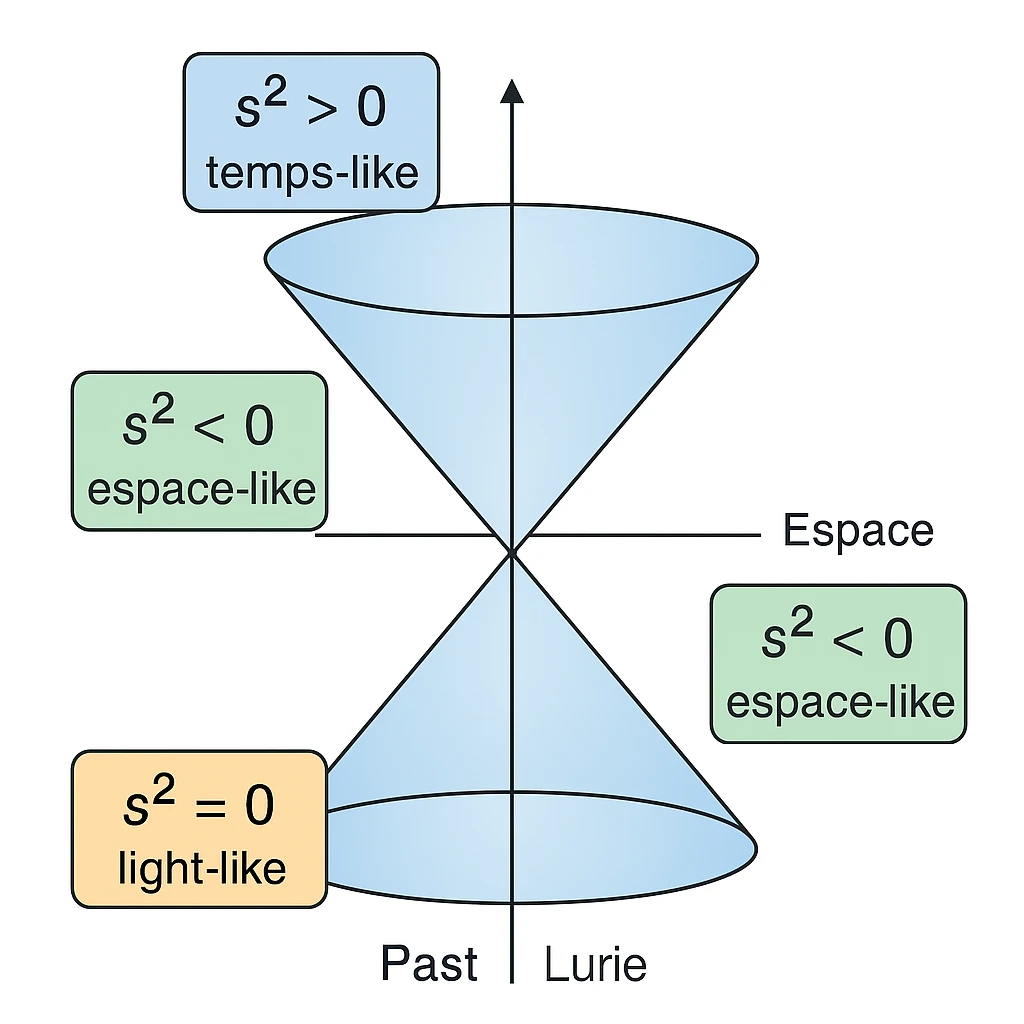
Die Beziehung \( s^2 = c^2 t^2 - x^2 - y^2 - z^2 \) ist bekannt alsMinkowski-Metrik. Es definiert ainvariantes Intervall (vierdimensionaler Abstand zwischen zwei Ereignissen in der Raumzeit)zwischen zwei Ereignissen imRaumzeit (kombination von drei Raumdimensionen und Zeit).

Dabei stellt \(c\) die Lichtgeschwindigkeit dar, \(t\) die von einem ruhenden Beobachter gemessene Zeit, und \((x, y, z)\) die räumlichen Koordinaten der Ereignisse. Die Invarianz von \(s^2\) impliziert dies alle Beobachter, unabhängig von ihrer relativen Bewegung oder Position, misst das gleiche vierdimensionale Intervall zwischen zwei Ereignissen.

Diese Metrik zeigt, dass Zeit und Raum keine getrennten Einheiten sind: eine Veränderung der Raumkoordinaten führt zu einer wirksamen Veränderung der wahrgenommenen Zeit, Phänomen bekannt alsZeitdilatation (zeitdilatation aufgrund relativer Bewegung oder Gravitation). Beispielsweise misst ein sich schnell bewegender Beobachter eine längere \(\Delta t\) Zeit zwischen zwei Ereignissen als ein ruhender Beobachter.

Diese mathematische Formalisierung bildet die Grundlage aller modernen Experimente zur Relativitätstheorie. ob sich Atomuhren bewegen oder GPS-Systeme, die eine Korrektur relativistischer Effekte erfordern.

Körperliche Folgen

Die bei schnellen Teilchen beobachtete Zeitdilatation oder die zeitliche Verlangsamung in der Nähe eines massiven Objekts, bestätigt, dass die vierte Dimension nicht nur ein abstraktes Konzept, sondern eine messbare physikalische Eigenschaft ist. Experimente mit Atomuhren im Flug oder im Orbit beweisen die Gültigkeit relativistischer Gleichungen mit einer Genauigkeit > 10^-15.

Übersichtstabelle

• Quellen:Albert-Einstein-Archiv (neues Fenster), Natur (neues Fenster), Wissenschaft (neues Fenster).