La géométrie du temps: explorer la quatrième dimension de l’Univers

Notion de temps

Depuis le début du XX^e siècle, la notion de temps a cessé d’être un simple paramètre universel, présent depuis toujours, pour devenir une dimension intégrée à la structure même de l’Univers. La théorie de la relativité restreinte, formulée en 1905 par Albert Einstein (1879-1955), a montré que la durée mesurée dépend du mouvement relatif de l’observateur. En 1915, la relativité générale a introduit la courbure de l’espace-temps (structure quadridimensionnelle combinant espace et temps) sous l’effet de la masse et de l’énergie.

Temps et espace réunis: une unité géométrique

L’espace-temps (ensemble des trois dimensions spatiales et du temps, formant une variété quadridimensionnelle) peut être décrit comme une variété à quatre dimensions où les événements possèdent des coordonnées \((x, y, z, ct)\). La métrique de Minkowski, qui formalise l’intervalle spatio-temporel de la relativité restreinte, a été formulée en 1908 par Hermann Minkowski (1864-1909).
Elle définit l’intervalle invariant: $$ \boxed{\color{blue}{\displaystyle s^2}} = (ct)^2 - x^2 - y^2 - z^2 $$
Cette relation montre que le temps et l’espace sont intimement liés, et que la géométrie du temps dépend de la vitesse de l’observateur ainsi que de la gravitation.

Pourquoi relier c et t dans les coordonnées de l'espace-temps ?

On écrit souvent les coordonnées d’un événement comme (x, y, z, ct) plutôt que (x, y, z, t) afin que la composante temporelle ct ait la même dimension (longueur) que les coordonnées spatiales.
Problème: x,y et z s’expriment en mètres, alors que ���� s’exprime en secondes → Impossible de les additionner directement dans une norme ou une distance.
La solution: multiplier ���� par ���� (vitesse de la lumière), qui a pour unité m/s: ��������[m]. Ainsi, ct est en mètres, comme x,y,z. Cette homogénéité rend l’intervalle de Minkowski, \( \boldsymbol{s^2} = (ct)^2 - x^2 - y^2 - z^2 \), plus compact et permet de représenter l’espace et le temps dans un même cadre géométrique à quatre dimensions.

La métrique de Minkowski et l’espace-temps

Type d’intervalle spatio-temporel

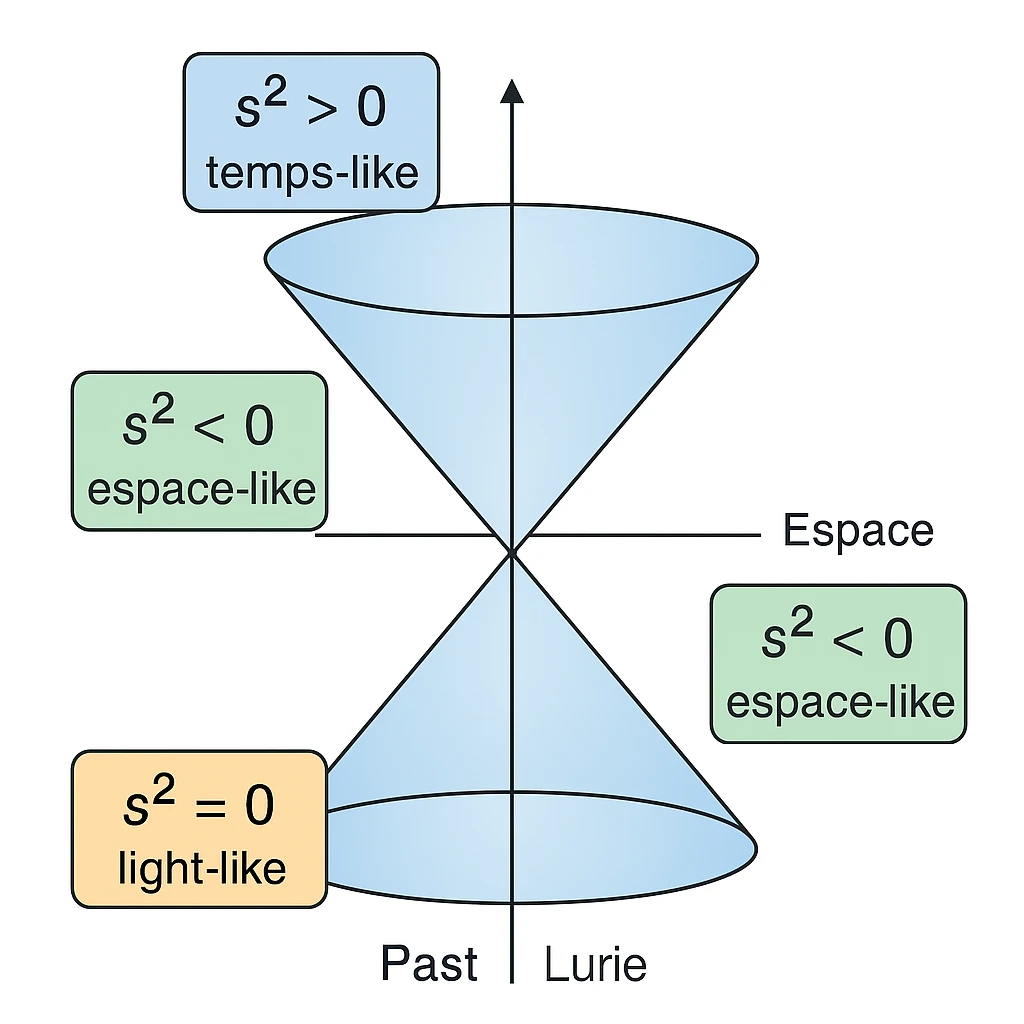
La relation \( s^2 = c^2 t^2 - x^2 - y^2 - z^2 \) est connue sous le nom de métrique de Minkowski. Elle définit un intervalle invariant (distance quadridimensionnelle entre deux événements dans l'espace-temps) entre deux événements dans l’espace-temps (combinaison des trois dimensions spatiales et du temps).

Ici, \(c\) représente la vitesse de la lumière, \(t\) le temps mesuré par un observateur au repos, et \((x, y, z)\) les coordonnées spatiales des événements. L’invariance de \(s^2\) implique que tous les observateurs, quels que soient leur mouvement relatif ou leur position, mesureront le même intervalle quadridimensionnel entre deux événements.

Cette métrique montre que le temps et l’espace ne sont pas des entités séparées: une modification des coordonnées spatiales entraîne une modification effective du temps perçu, phénomène connu sous le nom de dilatation temporelle (dilatation du temps due au mouvement relatif ou à la gravitation). Par exemple, un observateur en mouvement rapide mesurera un temps \(\Delta t\) plus long entre deux événements qu’un observateur au repos.

Cette formalisation mathématique constitue la base de toutes les expériences modernes sur la relativité, qu’il s’agisse des horloges atomiques en mouvement ou des systèmes GPS nécessitant une correction des effets relativistes.

Conséquences physiques

La dilatation du temps observée pour des particules rapides, ou le ralentissement temporel près d’un objet massif, confirme que la quatrième dimension n’est pas seulement un concept abstrait mais une propriété physique mesurable. Les expériences menées avec des horloges atomiques en vol ou en orbite démontrent la validité des équations relativistes avec une précision >10^-15.

Tableau récapitulatif

• Sources: Albert Einstein Archives (nouvelle fenêtre), Nature (nouvelle fenêtre), Science (nouvelle fenêtre).