L’astronomie grecque naît d’une transition majeure : celle du mythe vers la raison. Dès le VIIIe siècle BCE, les poèmes d’Hésiode et d’Homère évoquent un ciel peuplé de dieux et de constellations symboliques servant à rythmer les activités agricoles et maritimes. Mais à partir du VIe siècle BCE, les philosophes présocratiques introduisent une approche naturaliste du cosmos : Thalès de Milet, Anaximandre, Anaximène, Pythagore, Parménide, puis Anaxagore font des astres des objets matériels obéissant à des lois, remplaçant progressivement la mythologie par la raison.
Les premiers penseurs présocratiques tentèrent d’expliquer le cosmos de manière rationnelle. Thalès de Milet aurait prédit une éclipse solaire (probablement celle du 28 mai 585 BCE) et compris que la Lune brillait par la lumière du Soleil. Anaximandre proposa une Terre flottant librement dans l’espace, tandis qu’Anaximène identifia l’air comme principe fondamental de toute matière. Pythagore introduisit l’idée d’un univers gouverné par les nombres et l’harmonie, et Parménide souligna l’immobilité et l’unité de l’Être. Enfin, Anaxagore expliqua les éclipses et la nature du Soleil comme un corps incandescent, tout en postulant une intelligence ordonnatrice (Νοῦς signifie « Intelligence », « Esprit » ou « Raison ») régissant le cosmos.
Vers le Ve siècle BCE, les pythagoriciens introduisent la notion d’un ordre mathématique universel. Pour eux, « tout est nombre » et le cosmos (kosmos signifiant « ordre ») doit obéir à des rapports harmoniques. Ils conçoivent un univers sphérique où la Terre est immobile au centre, entourée de sphères cristallines portant les planètes et les étoiles.
Philolaos, disciple pythagoricien, fut l’un des premiers à suggérer que la Terre tournait autour d’un « feu central », anticipant une vision héliocentrique primitive. Mais c’est Aristote (384–322 BCE) qui systématisa la cosmologie géocentrique. Dans sa Physique et son De Caelo, il décrit un univers fini composé de sphères concentriques. La Terre, au centre, est immobile ; les corps célestes, faits d’« éther », se meuvent circulairement et éternellement.
N.B. :
Le modèle aristotélicien combine physique qualitative (éléments : terre, eau, air, feu, éther) et géométrie céleste. Il sera adopté pendant près de deux millénaires, jusqu’à Copernic (1543).
Pour décrire les mouvements irréguliers des planètes, Eudoxe de Cnide (vers 400–347 BCE) invente un système de sphères homocentriques : chaque planète est portée par un ensemble de sphères tournant à différentes vitesses. Bien que purement géométrique, ce modèle ouvre la voie à la modélisation mathématique du ciel.
Hipparque de Nicée (190–120 BCE), considéré comme le plus grand astronome de l’Antiquité, introduit la méthode trigonométrique et découvre la précession des équinoxes (\(\approx 50.3''\) par an). Il élabore le premier catalogue stellaire (850 étoiles) avec leurs coordonnées en latitude et longitude célestes.
Claude Ptolémée (IIe siècle CE), dans son traité Almageste, synthétise toute la science grecque en un système géocentrique à épicycles et déférents, permettant de reproduire avec précision les positions planétaires.
| Nom | Période | Contributions majeures | Concepts ou instruments |
|---|---|---|---|
| Thalès de Milet | vers 624 – 546 BCE | Prédit une éclipse solaire ; comprend que la Lune reflète la lumière du Soleil. | Observation directe et géométrie élémentaire. |
| Anaximandre | 610 – 546 BCE | Conçoit une Terre suspendue dans l’espace, première représentation cosmique en coupe. | Carte du monde, conception d’un cosmos cylindrique. |
| Anaximène | 585 – 525 BCE | Propose l’air comme principe fondamental ; décrit la formation des astres par condensation et raréfaction. | Observation et raisonnement naturaliste. |
| Pythagore et Philolaos | VIe – Ve siècle BCE | Harmonie des sphères ; hypothèse d’un feu central ; introduction des nombres comme principes cosmiques. | Modèle géométrique sphérique du cosmos. |
| Parménide | fin VIe – début Ve siècle BCE | Affirme l’immobilité et l’unité de l’Être ; influence sur la distinction entre apparence et réalité dans l’astronomie. | Raisonnement philosophique abstrait. |
| Anaxagore | 500 – 428 BCE | Explique les éclipses et la nature du Soleil comme corps incandescent ; introduit Nous comme intelligence organisatrice du cosmos. | Observation et raisonnement rationnel, principe ordonnateur immatériel. |
| Ératosthène | 276 – 194 BCE | Mesure la circonférence de la Terre à partir de la différence d’ombre à Alexandrie et Syène ; démontre la sphéricité de la Terre. | Géométrie des angles, distance entre villes, observation solaire au solstice. |
| Aristote | 384 – 322 BCE | Théorie géocentrique à sphères concentriques ; distinction entre monde sublunaire et supralunaire. | Physique à cinq éléments ; sphères cristallines. |
| Aristarque de Samos | 310 – 230 BCE | Propose un modèle héliocentrique ; estime la distance Terre–Soleil par trigonométrie. | Rapports angulaires \( \theta = \arctan(R_{\text{Terre–Lune}} / R_{\text{Soleil–Terre}}) \). |
| Eudoxe de Cnide | vers 408 – 355 BCE | Modèle géocentrique à 27 sphères concentriques pour expliquer les mouvements planétaires. | Sphères concentriques et géométrie mathématique. |
| Hipparque | 190 – 120 BCE | Découvre la précession des équinoxes ; établit le premier catalogue stellaire. | Trigonométrie sphérique, instruments d’observation (dioptra, astrolabe primitif). |
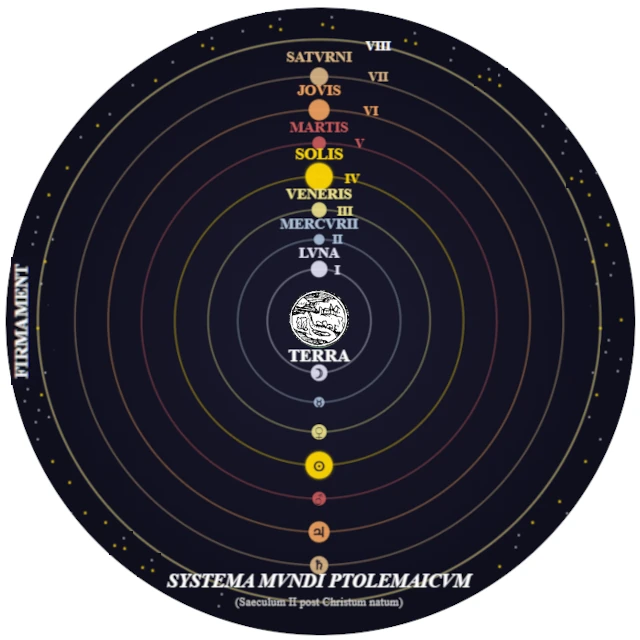
| Ptolémée | 100 – 170 CE | Modèle géocentrique à épicycles ; tables astronomiques précises. | Almageste ; instruments : astrolabe, armillaire. |
N.B. :
Le modèle de Ptolémée, bien qu’imparfait, permettait une précision de l’ordre de \( \pm 10' \) pour la position planétaire, remarquable pour des mesures à l’œil nu.
Les astronomes grecs mirent au point des instruments géométriques pour mesurer les angles célestes. Parmi eux, le gnomon pour déterminer la hauteur du Soleil et la latitude, le dioptre pour mesurer les angles, et surtout l’astrolabe, attribué à Hipparque puis perfectionné par Ptolémée.
Ces outils permettaient d’estimer les coordonnées célestes (\( \alpha, \delta \)) des étoiles et d’évaluer la taille de la Terre. Ératosthène (276–194 BCE), en comparant les ombres portées à Syène et Alexandrie au solstice d’été, calcula la circonférence terrestre : \( C = 360^\circ \times \frac{d}{7,2^\circ} = 39\,375\, \text{km} \approx R_{\text{Terre}} \times 2\pi \) une valeur étonnamment proche de la réalité moderne.
N.B. :
Ératosthène trouva \( R_{\text{Terre}} \approx 6,367\,\text{km} \), soit une erreur de moins de 1 % par rapport à la valeur actuelle (6,371 km). La distance réelle entre Alexandrie et Assouan est d’environ 840 km, mais l’unité exacte du stade qu’Ératosthène utilisait est approximativement comprise entre 157 et 185 m. La mesure de la circonférence terrestre (≈ 39 375 km ou ≈ 46 620 km selon la conversion) était proche de la valeur réelle de 40 075 km.
Après la chute d’Alexandrie et la fin du monde hellénistique, les textes grecs furent traduits et conservés par les savants arabes, notamment à Bagdad au IXe siècle. Les astronomes comme Al-Battani ou Al-Tusi révisèrent et améliorèrent les modèles ptolémaïques. Ce savoir sera ensuite transmis à l’Europe médiévale via Tolède et Cordoue.
Ainsi, la tradition grecque a fourni la structure conceptuelle de la cosmologie médiévale, avant que le modèle héliocentrique de Copernic (1543) ne rompe avec le géocentrisme.
L’astronomie grecque n’est pas seulement une science d’observation : elle représente une révolution intellectuelle. En introduisant la raison géométrique dans l’étude du ciel, elle a posé les fondations de la méthode scientifique occidentale.
Les Grecs ont inventé l’idée que l’Univers pouvait être compris par les mathématiques. De cette conviction découlera la physique moderne, de Kepler à Newton. Leur héritage perdure dans notre vocabulaire (planète, cosmos, sphère, zodiaque) et dans la structure même de notre pensée scientifique.
Références :
– D.R. Dicks, Early Greek Astronomy to Aristotle, Cornell University Press (1970).
– James Evans, The History and Practice of Ancient Astronomy, Oxford University Press (1998).
– Neugebauer, O., Astronomical Cuneiform Texts, Springer (1955).
– Toomer, G.J., Ptolemy’s Almagest, Princeton University Press (1984).
– Bowen & Todd, Aristarchus of Samos: The Ancient Copernicus, Oxford (2020).
Le Big Bang : Aux Frontières du Modèle 
Quand l’espace se courbe : la minuscule pente qui guide l’univers 
Astronomie Nabatéenne : Les maîtres du désert entre ciel étoilé et constructions de pierres 
Astronomie Polynésienne : L'Art de Naviguer à travers l'Océan Pacifique 
Astronomie Mésopotamienne : Le Berceau de l'Observation Céleste 
Astronomie Andine : Un Lien Sacré entre le Ciel et la Terre 
Astronomie Perse Antique : Entre Babylone et l'Âge d'Or Islamique 
Astronomie Maya : Les Cycles Célestes dictaient le Temps religieux, agricole et politique 
L'Astronomie Islamique : Quand Bagdad Illuminait le Ciel des Sciences 
L'Astronomie Indienne : Le passage de la poésie sacrée à la pensée scientifique 
L’Astronomie Grecque Antique : L'univers des philosophes en quête d'ordre cosmique 
Les Trois Formes Cosmiques : Une Géométrie Cachée de l’Univers 
L’Astronomie Égyptienne : Entre Ciel et Nil, les Secrets du Temps 
L’Astronomie Babylonienne : Quand le Ciel Prédisait le Destin 
L'Astronomie Impériale Chinoise : Un Héritage Scientifique Millénaire 
Objets Cosmiques Extrêmes : Là où la Physique Explose 
Univers miroir : Coexistence des deux mondes dans un reflet cosmique 
La première seconde de notre histoire 
La Dilatation du Temps : Mirage Relativiste ou Réalité ?
L'espace dans le temps : une notion en constante évolution 
L'Univers en Expansion : Que Signifie Vraiment "Créer de l'Espace" ? 
Du néant au cosmos : Pourquoi y a-t-il quelque chose plutôt que rien ? 
Glossaire Astronomie et Astrophysique : Définitions Clés et Concepts Fondamentaux 
Comment l’Univers peut mesurer 93 milliards d’années-lumière ? 
Comment peut-on affirmer que l'Univers a un âge ? 
Première preuve de l'Expansion de l'Univers 
Tranches d'espace-temps de l'Univers observable 
Âges sombres de l'Univers 
Théories alternatives à l'expansion accélérée de l'Univers 
L'atome primitif de l'abbé Georges Lemaître 
Grands murs et filaments : les grandes structures de l'Univers 
Aux Origines de l’Univers : Une Histoire des Représentations Cosmiques 
Bulles Lyman-alpha : Traces Gazeuses des Premières Galaxies 
Bouffées de Rayons Gamma : L’Ultime Soupir des Étoiles Géantes 
Perspective sur l’Inflation de l’Univers 
L'univers de Planck : l'image de l'univers se précise 
Le ciel est immense avec Laniakea 
Abondance des éléments chimiques dans l'Univers 
Les symétries de l'univers : Un voyage entre mathématiques et réalité physique 
La géométrie du temps : explorer la quatrième dimension de l’Univers 
Comment mesurer les distances dans l'Univers ? 
Pourquoi ‘rien’ est impossible : Le néant et le vide existent-ils ? 
Le Problème de l’Horizon : Comprendre l’Uniformité du Cosmos 
Qu'est-ce que la Matière Noire ? L’Invisible qui Structure l’Univers 
Métavers, l'étape suivante de l'évolution 
Multivers : Un Océan de Bulles d’Espace-Temps en Expansion 
La Recombinaison Cosmologique : quand l’Univers devint transparent 
Les constantes cosmologiques et physiques de notre Univers 
La thermodynamique du tas de sable et l'effet d'avalanche 
Le moteur de l'expansion accélérée de l'Univers 
L’Univers des Rayons X : Quand l’Espace Devient Transparent 
Les plus vieilles galaxies de l'univers 
Constante de Hubble et expansion de l'Univers 
Énergie noire : Quand l’Univers échappe à sa propre gravité 
Quelle est la taille de l’Univers ? Entre horizon cosmologique et infini 
Vide quantique et particules virtuelles : une réalité physique du rien 
Paradoxe de la nuit noire 
Voyage au cœur des paradoxes : les énigmes qui ont révolutionné la science 
Fond diffus cosmologique : L’écho thermique du Big Bang