Greek astronomy was born from a major transition: from myth to reason. From the 8th century BCE, the poems of Hesiod and Homer described a sky populated by gods and symbolic constellations, used to rhythm agricultural and maritime activities. But from the 6th century BCE, the pre-Socratic philosophers introduced a naturalistic approach to the cosmos: Thales of Miletus, Anaximander, Anaximenes, Pythagoras, Parmenides, and then Anaxagoras transformed celestial bodies into material objects obeying laws, gradually replacing mythology with reason.
The first pre-Socratic thinkers attempted to explain the cosmos rationally. Thales of Miletus is said to have predicted a solar eclipse (probably that of May 28, 585 BCE) and understood that the Moon shines by reflecting the Sun's light. Anaximander proposed that Earth floats freely in space, while Anaximenes identified air as the fundamental principle of all matter. Pythagoras introduced the idea of a universe governed by numbers and harmony, and Parmenides emphasized the immobility and unity of Being. Finally, Anaxagoras explained eclipses and the nature of the Sun as an incandescent body, while postulating an ordering intelligence (Νοῦς means "Intelligence," "Mind," or "Reason") governing the cosmos.
In the 5th century BCE, the Pythagoreans introduced the notion of a universal mathematical order. For them, "everything is number," and the cosmos (kosmos meaning "order") must obey harmonic ratios. They conceived of a spherical universe where Earth is immobile at the center, surrounded by crystalline spheres carrying the planets and stars.
Philolaus, a Pythagorean disciple, was one of the first to suggest that Earth revolved around a "central fire," anticipating a primitive heliocentric vision. But it was Aristotle (384–322 BCE) who systematized geocentric cosmology. In his Physics and De Caelo, he described a finite universe composed of concentric spheres. Earth, at the center, is immobile; celestial bodies, made of "aether," move circularly and eternally.
N.B.:
The Aristotelian model combines qualitative physics (elements: earth, water, air, fire, aether) and celestial geometry. It was adopted for nearly two millennia, until Copernicus (1543).
To describe the irregular movements of the planets, Eudoxus of Cnidus (c. 400–347 BCE) invented a system of homocentric spheres: each planet is carried by a set of spheres rotating at different speeds. Although purely geometric, this model paved the way for mathematical modeling of the sky.
Hipparchus of Nicaea (190–120 BCE), considered the greatest astronomer of antiquity, introduced trigonometric methods and discovered the precession of the equinoxes (\(\approx 50.3''\) per year). He developed the first star catalog (850 stars) with their celestial latitude and longitude coordinates.
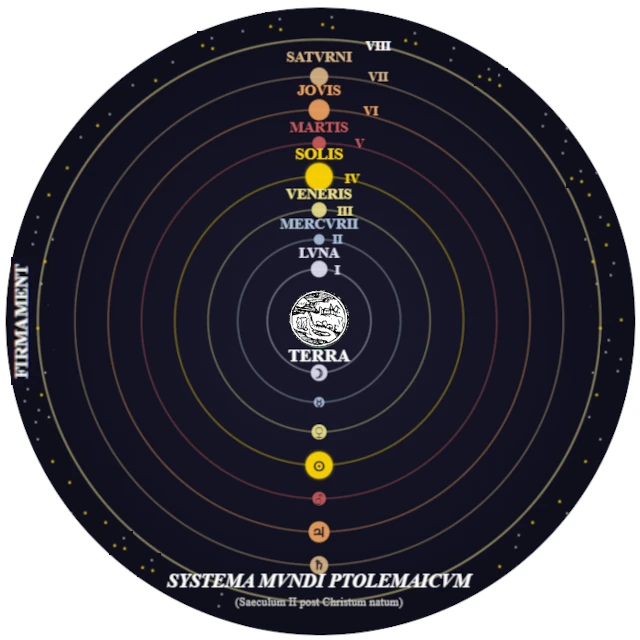
Claudius Ptolemy (2nd century CE), in his treatise Almagest, synthesized all Greek science into a geocentric system with epicycles and deferents, allowing precise reproduction of planetary positions.
| Name | Period | Major Contributions | Concepts or Instruments |
|---|---|---|---|
| Thales of Miletus | c. 624 – 546 BCE | Predicted a solar eclipse; understood that the Moon reflects the Sun's light. | Direct observation and elementary geometry. |
| Anaximander | 610 – 546 BCE | Conceived of Earth suspended in space, first cosmic cross-section representation. | World map, conception of a cylindrical cosmos. |
| Anaximenes | 585 – 525 BCE | Proposed air as the fundamental principle; described the formation of stars by condensation and rarefaction. | Observation and naturalistic reasoning. |
| Pythagoras and Philolaus | 6th – 5th century BCE | Harmony of the spheres; hypothesis of a central fire; introduction of numbers as cosmic principles. | Spherical geometric model of the cosmos. |
| Parmenides | late 6th – early 5th century BCE | Asserted the immobility and unity of Being; influenced the distinction between appearance and reality in astronomy. | Abstract philosophical reasoning. |
| Anaxagoras | 500 – 428 BCE | Explained eclipses and the nature of the Sun as an incandescent body; introduced Nous as the organizing intelligence of the cosmos. | Observation and rational reasoning, immaterial ordering principle. |
| Eratosthenes | 276 – 194 BCE | Measured Earth's circumference from the difference in shadows at Alexandria and Syene; demonstrated Earth's sphericity. | Angle geometry, distance between cities, solar observation at solstice. |
| Aristotle | 384 – 322 BCE | Geocentric theory with concentric spheres; distinction between sublunary and supralunary worlds. | Physics of five elements; crystalline spheres. |
| Aristarchus of Samos | 310 – 230 BCE | Proposed a heliocentric model; estimated the Earth-Sun distance using trigonometry. | Angular ratios \( \theta = \arctan(R_{\text{Earth–Moon}} / R_{\text{Sun–Earth}}) \). |
| Eudoxus of Cnidus | c. 408 – 355 BCE | Geocentric model with 27 concentric spheres to explain planetary movements. | Concentric spheres and mathematical geometry. |
| Hipparchus | 190 – 120 BCE | Discovered the precession of the equinoxes; established the first star catalog. | Spherical trigonometry, observation instruments (dioptra, primitive astrolabe). |
| Ptolemy | 100 – 170 CE | Geocentric model with epicycles; precise astronomical tables. | Almagest; instruments: astrolabe, armillary sphere. |
N.B.:
Ptolemy's model, although imperfect, allowed for planetary position accuracy of about \( \pm 10' \), remarkable for naked-eye measurements.
Greek astronomers developed geometric instruments to measure celestial angles. Among them, the gnomon to determine the height of the Sun and latitude, the dioptra to measure angles, and especially the astrolabe, attributed to Hipparchus and later perfected by Ptolemy.
These tools allowed estimating celestial coordinates (\( \alpha, \delta \)) of stars and evaluating the size of Earth. Eratosthenes (276–194 BCE), by comparing shadows at Syene and Alexandria during the summer solstice, calculated Earth's circumference: \( C = 360^\circ \times \frac{d}{7.2^\circ} = 39,375\, \text{km} \approx R_{\text{Earth}} \times 2\pi \) a value surprisingly close to modern reality.
N.B.:
Eratosthenes found \( R_{\text{Earth}} \approx 6,367\,\text{km} \), an error of less than 1% compared to the current value (6,371 km). The actual distance between Alexandria and Aswan is about 840 km, but the exact unit of the stadium Eratosthenes used is approximately between 157 and 185 m. The measurement of Earth's circumference (≈ 39,375 km or ≈ 46,620 km depending on conversion) was close to the real value of 40,075 km.
After the fall of Alexandria and the end of the Hellenistic world, Greek texts were translated and preserved by Arab scholars, notably in Baghdad in the 9th century. Astronomers such as Al-Battani or Al-Tusi revised and improved Ptolemaic models. This knowledge was then transmitted to medieval Europe via Toledo and Cordoba.
Thus, the Greek tradition provided the conceptual framework for medieval cosmology, before Copernicus' heliocentric model (1543) broke with geocentrism.
Greek astronomy is not just an observational science: it represents an intellectual revolution. By introducing geometric reason into the study of the sky, it laid the foundations of the Western scientific method.
The Greeks invented the idea that the Universe could be understood through mathematics. From this conviction would emerge modern physics, from Kepler to Newton. Their legacy endures in our vocabulary (planet, cosmos, sphere, zodiac) and in the very structure of our scientific thought.
References:
– D.R. Dicks, Early Greek Astronomy to Aristotle, Cornell University Press (1970).
– James Evans, The History and Practice of Ancient Astronomy, Oxford University Press (1998).
– Neugebauer, O., Astronomical Cuneiform Texts, Springer (1955).
– Toomer, G.J., Ptolemy’s Almagest, Princeton University Press (1984).
– Bowen & Todd, Aristarchus of Samos: The Ancient Copernicus, Oxford (2020).
Ancient Greek Astronomy: The Universe of Philosophers in Search of Cosmic Order 
The Three Cosmic Shapes: A Hidden Geometry of the Universe 
Egyptian Astronomy: Between Sky and Nile, the Secrets of Time 
Babylonian Astronomy: When the Sky Predicted Destiny 
Chinese Imperial Astronomy: A Millennial Scientific Legacy 
Extreme Cosmic Objects: Where Physics Explodes 
Mirror Universe: Coexistence of Two Worlds in a Cosmic Reflection 
The first second of our history 
Time Dilation: Relativistic Mirage or Reality?
Space Through Time: A Constantly Evolving Concept
The Expanding Universe: What Does "Creating Space" Really Mean? 
From Nothingness to the Cosmos: Why Is There Something Rather Than Nothing? 
Glossary of Astronomy and Astrophysics: Key Definitions and Fundamental Concepts 
How can the Universe measure 93 billion light-years? 
How can we say that the Universe has an age? 
First Proof of the Expansion of the Universe 
Space-time slices of the observable Universe 
Dark Ages of the Universe 
Alternative theories to the accelerated expansion of the universe 
The primitive atom of Abbot Georges Lemaître 
Great walls and filaments: the great structures of the Universe 
The Origins of the Universe: A History of Cosmic Representations 
Lyman-alpha Blobs: Gaseous Traces of the First Galaxies 
Gamma-Ray Bursts: The Ultimate Breath of Giant Stars 
Perspective on the Inflation of the Universe 
The Planck Universe: the Image of the Universe Becomes Clearer
The sky is immense with Laniakea 
Abundance of chemical elements in the Universe 
The Symmetries of the Universe: A Journey Between Mathematics and Physical Reality 
The Geometry of Time: Exploring the Fourth Dimension of the Universe 
How to measure distances in the Universe? 
Why ‘nothing’ is impossible: Do nothingness and emptiness exist? 
The Horizon Problem: Understanding the Uniformity of the Cosmos 
What is Dark Matter? The Invisible Force Shaping the Universe 
Metaverse, the next stage of evolution 
Multiverse: An Ocean of Expanding Space-Time Bubbles 
Cosmological Recombination: When the Universe Became Transparent 
The cosmological and physical constants of our Universe 
The Thermodynamics of the Sandpile and the Avalanche Effect 
The engine of the accelerated expansion of the Universe 
The X-Ray Universe: When Space Becomes Transparent 
The oldest galaxies in the universe 
Hubble constant and expansion of the Universe 
Dark Energy: When the Universe Defies Its Own Gravity 
What is the Size of the Universe? Between Cosmological Horizon and Infinity 
Quantum Vacuum and Virtual Particles: The Physical Reality of Nothingness 
Paradox of the dark night 
Journey into the Heart of Paradoxes: The Enigmas That Revolutionized Science 
Cosmic Microwave Background: The Thermal Echo of the Big Bang