A astronomia grega nasceu de uma transição significativa: do mito à razão. Desde o século VIII a.C., os poemas de Hesíodo e Homero descreviam um céu povoado de deuses e constelações simbólicas, usadas para ritmar as atividades agrícolas e marítimas. Mas a partir do século VI a.C., os filósofos pré-socráticos introduziram uma abordagem naturalista do cosmos: Tales de Mileto, Anaximandro, Anaximenes, Pitágoras, Parmênides e depois Anaxágoras transformaram os astros em objetos materiais que obedecem a leis, substituindo gradualmente a mitologia pela razão.
Os primeiros pensadores pré-socráticos tentaram explicar o cosmos de maneira racional. Tales de Mileto teria previsto um eclipse solar (provavelmente o de 28 de maio de 585 a.C.) e compreendeu que a Lua brilha refletindo a luz do Sol. Anaximandro propôs uma Terra flutuando livremente no espaço, enquanto Anaximenes identificou o ar como o princípio fundamental de toda matéria. Pitágoras introduziu a ideia de um universo governado por números e harmonia, e Parmênides enfatizou a imobilidade e a unidade do Ser. Finalmente, Anaxágoras explicou os eclipses e a natureza do Sol como um corpo incandescente, postulando uma inteligência ordenadora (Νοῦς significa "Inteligência", "Espírito" ou "Razão") que rege o cosmos.
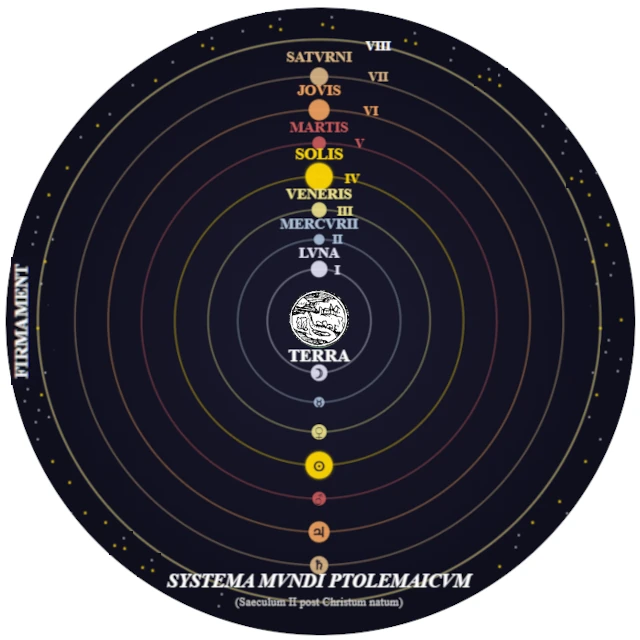
Por volta do século V a.C., os pitagóricos introduziram a noção de uma ordem matemática universal. Para eles, "tudo é número" e o cosmos (kosmos significa "ordem") deve obedecer a relações harmônicas. Conceberam um universo esférico onde a Terra está imóvel no centro, cercada por esferas cristalinas que carregam os planetas e as estrelas.
Filolau, discípulo pitagórico, foi um dos primeiros a sugerir que a Terra girava em torno de um "fogo central", antecipando uma visão heliocêntrica primitiva. Mas foi Aristóteles (384–322 a.C.) quem sistematizou a cosmologia geocêntrica. Em sua Física e De Caelo, descreveu um universo finito composto por esferas concêntricas. A Terra, no centro, é imóvel; os corpos celestes, feitos de "éter", movem-se circular e eternamente.
N.B.:
O modelo aristotélico combina física qualitativa (elementos: terra, água, ar, fogo, éter) e geometria celestial. Foi adotado por quase dois milênios, até Copérnico (1543).
Para descrever os movimentos irregulares dos planetas, Eudoxo de Cnido (c. 400–347 a.C.) inventou um sistema de esferas homocêntricas: cada planeta é carregado por um conjunto de esferas girando em diferentes velocidades. Embora puramente geométrico, este modelo abriu caminho para a modelagem matemática do céu.
Hiparco de Niceia (190–120 a.C.), considerado o maior astrônomo da Antiguidade, introduziu métodos trigonométricos e descobriu a precessão dos equinócios (\(\approx 50.3''\) por ano). Ele elaborou o primeiro catálogo estelar (850 estrelas) com suas coordenadas de latitude e longitude celestes.
Claúdio Ptolomeu (século II d.C.), em seu tratado Almagesto, sintetizou toda a ciência grega em um sistema geocêntrico com epiciclos e deferentes, permitindo reproduzir com precisão as posições planetárias.
| Nome | Período | Contribuições principais | Conceitos ou instrumentos |
|---|---|---|---|
| Tales de Mileto | c. 624 – 546 a.C. | Previu um eclipse solar; compreendeu que a Lua reflete a luz do Sol. | Observação direta e geometria elementar. |
| Anaximandro | 610 – 546 a.C. | Concebeu uma Terra suspensa no espaço, primeira representação cósmica em corte. | Mapa do mundo, concepção de um cosmos cilíndrico. |
| Anaximenes | 585 – 525 a.C. | Propôs o ar como princípio fundamental; descreveu a formação dos astros por condensação e rarefação. | Observação e raciocínio naturalista. |
| Pitágoras e Filolau | séculos VI – V a.C. | Harmonia das esferas; hipótese de um fogo central; introdução dos números como princípios cósmicos. | Modelo geométrico esférico do cosmos. |
| Parmênides | final do século VI – início do V a.C. | Afirmou a imobilidade e a unidade do Ser; influenciou a distinção entre aparência e realidade na astronomia. | Raciocínio filosófico abstrato. |
| Anaxágoras | 500 – 428 a.C. | Explicou os eclipses e a natureza do Sol como corpo incandescente; introduziu Nous como inteligência organizadora do cosmos. | Observação e raciocínio racional, princípio ordenador imaterial. |
| Eratóstenes | 276 – 194 a.C. | Mediu a circunferência da Terra a partir da diferença de sombras em Alexandria e Siene; demonstrou a esfericidade da Terra. | Geometria dos ângulos, distância entre cidades, observação solar no solstício. |
| Aristóteles | 384 – 322 a.C. | Teoria geocêntrica com esferas concêntricas; distinção entre mundo sublunar e supralunar. | Física dos cinco elementos; esferas cristalinas. |
| Aristarco de Samos | 310 – 230 a.C. | Propôs um modelo heliocêntrico; estimou a distância Terra–Sol por trigonometria. | Relações angulares \( \theta = \arctan(R_{\text{Terra–Lua}} / R_{\text{Sol–Terra}}) \). |
| Eudoxo de Cnido | c. 408 – 355 a.C. | Modelo geocêntrico com 27 esferas concêntricas para explicar os movimentos planetários. | Esferas concêntricas e geometria matemática. |
| Hiparco | 190 – 120 a.C. | Descobriu a precessão dos equinócios; estabeleceu o primeiro catálogo estelar. | Trigonometria esférica, instrumentos de observação (dioptra, astrolábio primitivo). |
| Ptolomeu | 100 – 170 d.C. | Modelo geocêntrico com epiciclos; tabelas astronômicas precisas. | Almagesto; instrumentos: astrolábio, esfera armilar. |
N.B.:
O modelo de Ptolomeu, embora imperfeito, permitia uma precisão de cerca de \( \pm 10' \) para a posição planetária, notável para medições a olho nu.
Os astrônomos gregos desenvolveram instrumentos geométricos para medir os ângulos celestes. Entre eles, o gnômon para determinar a altura do Sol e a latitude, o dioptra para medir ângulos, e especialmente o astrolábio, atribuído a Hiparco e depois aperfeiçoado por Ptolomeu.
Essas ferramentas permitiam estimar as coordenadas celestes (\( \alpha, \delta \)) das estrelas e avaliar o tamanho da Terra. Eratóstenes (276–194 a.C.), ao comparar as sombras em Siene e Alexandria durante o solstício de verão, calculou a circunferência terrestre: \( C = 360^\circ \times \frac{d}{7.2^\circ} = 39,375\, \text{km} \approx R_{\text{Terra}} \times 2\pi \) um valor surpreendentemente próximo da realidade moderna.
N.B.:
Eratóstenes encontrou \( R_{\text{Terra}} \approx 6,367\,\text{km} \), um erro de menos de 1% em comparação com o valor atual (6,371 km). A distância real entre Alexandria e Assuã é de aproximadamente 840 km, mas a unidade exata do estádio que Eratóstenes usou está aproximadamente entre 157 e 185 m. A medição da circunferência terrestre (≈ 39,375 km ou ≈ 46,620 km dependendo da conversão) estava próxima do valor real de 40,075 km.
Após a queda de Alexandria e o fim do mundo helenístico, os textos gregos foram traduzidos e preservados pelos sábios árabes, especialmente em Bagdá no século IX. Astrônomos como Al-Battani ou Al-Tusi revisaram e melhoraram os modelos ptolomaicos. Esse conhecimento foi então transmitido à Europa medieval através de Toledo e Córdoba.
Assim, a tradição grega forneceu a estrutura conceitual da cosmologia medieval, antes que o modelo heliocêntrico de Copérnico (1543) rompesse com o geocentrismo.
A astronomia grega não é apenas uma ciência de observação: representa uma revolução intelectual. Ao introduzir a razão geométrica no estudo do céu, estabeleceu as bases do método científico ocidental.
Os gregos inventaram a ideia de que o Universo poderia ser compreendido através da matemática. Dessa convicção surgiria a física moderna, de Kepler a Newton. Seu legado perdura em nosso vocabulário (planeta, cosmos, esfera, zodíaco) e na própria estrutura de nosso pensamento científico.
Referências:
– D.R. Dicks, Early Greek Astronomy to Aristotle, Cornell University Press (1970).
– James Evans, The History and Practice of Ancient Astronomy, Oxford University Press (1998).
– Neugebauer, O., Astronomical Cuneiform Texts, Springer (1955).
– Toomer, G.J., Ptolemy’s Almagest, Princeton University Press (1984).
– Bowen & Todd, Aristarchus of Samos: The Ancient Copernicus, Oxford (2020).
Astronomia Grega Antiga: O universo dos filósofos em busca da ordem cósmica 
As Três Formas Cósmicas: Uma Geometria Oculta do Universo 
A Astronomia Egípcia: Entre o Céu e o Nilo, os Segredos do Tempo 
A Astronomia Babilônica: Quando o Céu Predizia o Destino 
A Astronomia Imperial Chinesa: Um Legado Científico Milenar 
Objetos Cósmicos Extremos: Onde a Física Explode 
Universo espelho: Coexistência de dois mundos em um reflexo cósmico 
O primeiro segundo da nossa história 
Dilatação do Tempo: Miragem Relativística ou Realidade?
O espaço ao longo do tempo: um conceito em constante evolução 
O Universo em Expansão: O Que Significa Realmente "Criar Espaço"? 
Do nada ao cosmos: Por que há algo em vez de nada? 
Glossário de Astronomia e Astrofísica: Definições-Chave e Conceitos Fundamentais 
Como o Universo pode medir 93 bilhões de anos-luz? 
Como podemos afirmar que o Universo tem uma idade? 
Primeira prova da expansão do universo 
Fatias de espaço-tempo no Universo observável 
Idade das Trevas do Universo 
Teorias alternativas à expansão acelerada do universo 
O átomo primitivo do Abade Georges Lemaître 
Grandes Muralhas e Filamentos: as grandes estruturas do Universo 
As Origens do Universo: Uma História das Representações Cósmicas 
Bolhas Lyman-alpha: Rastros Gasosos das Primeiras Galáxias 
Explosões de Raios Gama: O Último Suspiro das Estrelas Gigantes
Perspectiva sobre a Inflação do Universo 
O Universo de Planck: a Imagem do Universo se Torna Mais Clara
O céu é imenso com Laniakea 
Abundância de elementos químicos no Universo 
As simetrias do universo: Uma viagem entre matemática e realidade física 
A geometria do tempo: explorar a quarta dimensão do Universo 
Como medir distâncias no Universo? 
Por que ‘nada’ é impossível: O nada e o vazio existem? 
O Problema do Horizonte: Compreendendo a Uniformidade do Cosmos 
O que é a Matéria Escura? O Invisível que Estrutura o Universo 
Metaverso, o próximo estágio de evolução 
Multiverso: Um oceano de bolhas de espaço-tempo em expansão 
Recombinação Cosmológica: Quando o Universo se Tornou Transparente 
As constantes cosmológicas e físicas do nosso Universo 
A termodinâmica da pilha de areia e o efeito avalanche 
O motor da expansão acelerada do Universo 
O Universo de Raios X: Quando o Espaço se Torna Transparente 
As galáxias mais antigas do universo 
Constante de Hubble e expansão do Universo 
Energia Escura: Quando o Universo Escapa à Sua Própria Gravidade 
Qual é o tamanho do Universo? Entre o horizonte cosmológico e o infinito 
Vácuo quântico e partículas virtuais: a realidade física do nada 
Paradoxo da noite escura 
Viagem ao coração dos paradoxos: os enigmas que revolucionaram a ciência 
Radiação Cósmica de Fundo: O Eco Térmico do Big Bang