最終更新日：2025年11月13日

古代ギリシャ天文学：宇宙の秩序を求めた哲学者たちの宇宙

プトレマイオスによる地球中心の宇宙の表現 — 画像の説明：**地球中心の宇宙**（紀元前5世紀）の**プトレマイオス**（100-168年）による表現。地球が中心にあり、惑星と恒星の球体に囲まれています。
画像ソース：astronoo.com

宇宙の神話から合理的思考へ

ギリシャ天文学は大きな転換から生まれました：神話から理性への転換です。紀元前8世紀、ヘシオドスとホメロスの詩は、神々と象徴的な星座が住む天空を描き、農業や航海の活動をリズムづけていました。しかし、紀元前6世紀から、ソクラテス以前の哲学者たちは宇宙に自然主義的なアプローチを導入しました： タレス、アナクシマンドロス、アナクシメネス、ピタゴラス、パルメニデス、そしてアナクサゴラスは、天体を法則に従う物質的な対象とし、徐々に神話を理性に置き換えました。

最初のソクラテス以前の思想家たちは、宇宙を合理的に説明しようと試みました。 タレスは日食を予測した（おそらく紀元前585年5月28日の日食）とされ、月が太陽の光を反射して輝くことを理解しました。 アナクシマンドロスは、地球が宇宙空間に自由に浮かんでいると提案し、アナクシメネスは空気をすべての物質の基本原理と特定しました。 ピタゴラスは、数と調和によって支配される宇宙の概念を導入し、パルメニデスは存在の不動性と統一性を強調しました。最後に、アナクサゴラスは日食と太陽の本質を白熱する天体として説明し、宇宙を支配する知性（Νοῦςは「知性」、「精神」、「理性」を意味します）を仮定しました。

ピタゴラスからアリストテレスへ：宇宙の幾何学化

紀元前5世紀、ピタゴラス教団は普遍的な数学的秩序の概念を導入しました。彼らにとって、「すべては数である」と宇宙（kosmosは「秩序」を意味する）は調和の比率に従わなければなりません。彼らは球形の宇宙を構想しました。地球は中心に静止し、惑星や恒星を運ぶ結晶球体に囲まれています。

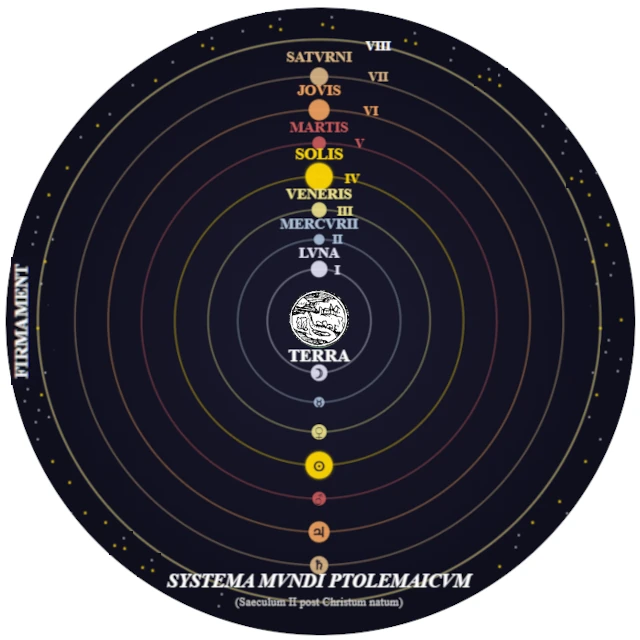
ピタゴラス教団の弟子であるフィロラオスは、地球が「中心の火」の周りを回っていると最初に示唆し、原始的な地動説のビジョンを予見しました。しかし、アリストテレス（紀元前384–322年）が地球中心説の宇宙論を体系化しました。彼の物理学と天についてでは、同心円の球体からなる有限の宇宙を描いています。地球は中心に静止し、天体は「エーテル」でできており、円形で永遠に動きます。

注：
アリストテレスのモデルは質的物理学（要素：地、水、空気、火、エーテル）と天体の幾何学を組み合わせています。このモデルはコペルニクス（1543年）まで、ほぼ2000年間採用されました。

数学的モデル：エウドクソスからプトレマイオスへ

惑星の不規則な動きを説明するために、クニドスのエウドクソス（紀元前400–347年頃）は同心球のシステムを発明しました：各惑星は異なる速度で回転する球体のセットによって運ばれます。純粋に幾何学的ではありますが、このモデルは天空の数学的モデリングへの道を開きました。

主なギリシャの天文学者

主なギリシャの天文学者とその主要な貢献
名前	時期	主要な貢献	概念または器具
タレス	紀元前624 – 546年頃	日食を予測；月が太陽の光を反射することを理解。	直接観測と初歩的な幾何学。
アナクシマンドロス	紀元前610 – 546年	宇宙空間に浮かぶ地球を構想；最初の宇宙の断面図。	世界地図、円筒形の宇宙の概念。
アナクシメネス	紀元前585 – 525年	空気を基本原理として提案；凝縮と希薄化による天体の形成を説明。	観測と自然主義的推論。
ピタゴラスとフィロラオス	紀元前6 – 5世紀	天体の調和；中心の火の仮説；数を宇宙の原理として導入。	宇宙の球形幾何学モデル。
パルメニデス	紀元前6世紀末 – 5世紀初頭	存在の不動性と統一性を主張；天文学における外観と現実の区別に影響。	抽象的な哲学的推論。
アナクサゴラス	紀元前500 – 428年	日食と太陽の本質を白熱する天体として説明；ヌースを宇宙の秩序付ける知性として導入。	観測と合理的推論、非物質的秩序原理。
エラトステネス	紀元前276 – 194年	アレクサンドリアとシエネの影の違いから地球の円周を測定；地球の球形を証明。	角度の幾何学、都市間の距離、夏至の太陽観測。
アリストテレス	紀元前384 – 322年	同心円の地球中心説；月下界と月上界の区別。	五元素の物理学；結晶球体。
サモスのアリスタルコス	紀元前310 – 230年	太陽中心説のモデルを提案；三角法による地球–太陽間の距離を推定。	角度比 \( \theta = \arctan(R_{\text{地球–月}} / R_{\text{太陽–地球}}) \)。
クニドスのエウドクソス	紀元前408 – 355年頃	惑星の動きを説明するための27の同心円モデル。	同心円と数学的幾何学。
ヒッパルコス	紀元前190 – 120年	分点の歳差運動を発見；最初の星表を作成。	球面三角法、観測器具（ディオプトラ、原始的なアストロラーベ）。
プトレマイオス	100 – 170年	周転円を持つ地球中心説；精密な天文表。	アルマゲスト；器具：アストロラーベ、天球儀。

注：
プトレマイオスのモデルは不完全ではありましたが、肉眼観測による惑星の位置精度は約 \( \pm 10' \) で、注目に値します。

観測と測定の器具

ギリシャの天文学者たちは、天体の角度を測定するための幾何学的器具を開発しました。その中には、太陽の高度と緯度を決定するためのグノーモン、角度を測定するためのディオプトラ、そして特にヒッパルコスに帰せられ、後にプトレマイオスによって改良されたアストロラーベがありました。

これらの器具は、星の天体座標（\( \alpha, \delta \)）を推定し、地球の大きさを評価することを可能にしました。 エラトステネス（紀元前276–194年）は、夏至のシエネとアレクサンドリアの影を比較することで地球の円周を計算しました： \( C = 360^\circ \times \frac{d}{7.2^\circ} = 39,375\, \text{km} \approx R_{\text{地球}} \times 2\pi \) この値は現代の実測値に驚くほど近いものです。

注：
エラトステネスは \( R_{\text{地球}} \approx 6,367\,\text{km} \) と求め、これは現在の値（6,371 km）と比べて1%未満の誤差です。アレクサンドリアとアスワンの間の実際の距離は約840 kmですが、エラトステネスが使用したスタディオンの正確な単位は約157から185 mの間と推定されます。地球の円周の測定値（≈ 39,375 kmまたは≈ 46,620 km、変換による）は、実際の値40,075 kmに近いものでした。

ギリシャの知識からアラビアとラテンへの伝達

アレクサンドリアの没落とヘレニズム世界の終わりの後、ギリシャのテキストはアラビアの学者たち、特に9世紀のバグダードによって翻訳され保存されました。 アル・バッターニーやアル・トゥーシーのような天文学者たちはプトレマイオスのモデルを改訂・改良しました。この知識はその後、トレドとコルドバを通じて中世ヨーロッパに伝えられました。

このように、ギリシャの伝統は中世の宇宙論の概念的枠組みを提供し、その後コペルニクスの太陽中心説モデル（1543年）が地球中心説を打破しました。

科学的および哲学的遺産

ギリシャ天文学は単なる観測科学ではありません：それは知的革命を表しています。天空の研究に幾何学的理性を導入することで、西洋の科学的方法の基礎を築きました。

ギリシャ人は宇宙は数学によって理解できるという考えを発明しました。この信念から、ケプラーからニュートンまでの近代物理学が生まれました。彼らの遺産は、私たちの語彙（惑星、宇宙、球体、黄道）や科学的思考の構造そのものに今も残っています。

参考文献：
– D.R. Dicks, Early Greek Astronomy to Aristotle, Cornell University Press (1970).
– James Evans, The History and Practice of Ancient Astronomy, Oxford University Press (1998).
– Neugebauer, O., Astronomical Cuneiform Texts, Springer (1955).
– Toomer, G.J., Ptolemy’s Almagest, Princeton University Press (1984).
– Bowen & Todd, Aristarchus of Samos: The Ancient Copernicus, Oxford (2020).