最終更新日: 2025 年 9 月 11 日

時間の幾何学: 宇宙の 4 次元の探求

時空のイラスト — *の曲率時空内容によって歪んだ織物として表現されます。画像出典:astronoo.com*

時間の概念

20世紀初頭以降^e世紀、という概念時間常に存在する単純な普遍的なパラメーターではなくなり、宇宙の構造そのものに統合された次元になりました。特殊相対性理論は 1905 年に定式化されました。アルバート・アインシュタイン(1879-1955) は、測定された持続時間が観察者の相対的な動きに依存することを示しました。 1915 年、一般相対性理論は、時空質量とエネルギーの影響下で。

時間と空間の結合: 幾何学的結合

L'時空は、イベントが座標 $(x, y, z, ct)$ を持つ 4 次元多様体として説明できます。ミンコフスキー指標。時空の間隔特殊相対性理論は 1908 年に定式化されました。ヘルマン・ミンコフスキー（1864-1909）。
不変間隔を定義します。 $$ \boxed{\color{blue}{\displaystyle s^2}} = (ct)^2 - x^2 - y^2 - z^2 $$
この関係は、時間と空間が密接に結びついていること、そして時間の幾何学的構造が観測者の速度と重力に依存します。

なぜ時空座標で c と t を関係付けるのでしょうか?

私たちはよくイベントの座標を次のように書きます。(x、y、z、ct)(x, y, z, t) ではなく、時間成分ct空間座標と同じ寸法 (長さ) を持ちます。
問題：x、y、zはメートル、��は秒で表現 → 規格や距離で直接加算することはできません。
解決策:�� に �� (光の速度) を掛けます。単位は m/s: ��[m] です。したがって、ct は x、y、z のようにメートル単位です。この均一性がミンコフスキー区間を作り、 $ \boldsymbol{s^2} = (ct)^2 - x^2 - y^2 - z^2 $ よりコンパクトになり、同じ 4 次元の幾何学的枠組みで空間と時間を表現できるようになります。

ミンコフスキー計量と時空

時空間隔の種類

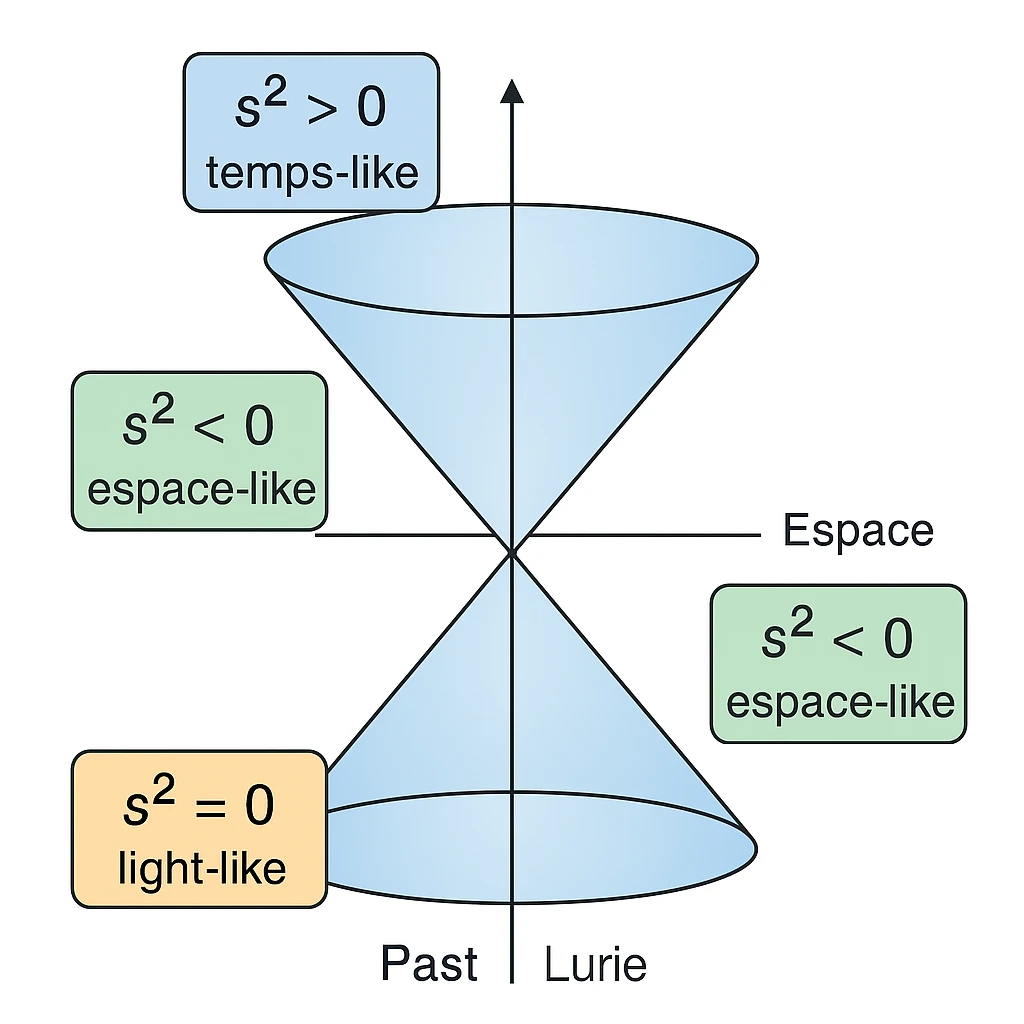
関係 $ s^2 = c^2 t^2 - x^2 - y^2 - z^2 $ として知られていますミンコフスキー指標。それは、不変区間の 2 つのイベントの間に時空。

ここで、 $c$ は光の速度、 $t$ は静止している観測者によって測定された時間を表します。 $(x, y, z)$ イベントの空間座標。 $s^2$ が不変であるということは、次のことを意味します。すべての観察者は、相対的な動きや位置に関係なく、 2 つのイベント間の同じ 4 次元間隔を測定します。

このメトリクスは、時間と空間が別個のエンティティではないことを示しています。空間座標の変更は、知覚される時間の効果的な変更につながります。として知られる現象時間の遅れ。たとえば、急速に移動している観測者は、静止している観測者よりも 2 つのイベント間の $\Delta t$ 時間を測定します。

この数学的形式化は、相対性理論に関する現代のすべての実験の基礎を構成します。移動原子時計であっても、相対論的効果の補正が必要な GPS システムであっても。

身体的な影響

高速粒子で観察される時間の遅れ、または大質量天体の近くでの時間の減速、 4 次元は単なる抽象的な概念ではなく、測定可能な物理的特性であることが確認されています。飛行中または軌道上で原子時計を使って行われた実験は、相対論的方程式の妥当性を実証します精度 > 10^-15。

科学 / コンセプト	貢献	年	参照
ヘルマン・ミンコフスキー (1864-1909)	幾何学的構造としての時空の導入	1908年	ミンコフスキー、ケルンでの会議 (1908)
アルバート・アインシュタイン (1879-1955)	特殊相対性理論: 時間と動きの関係	1905年	アインシュタイン A.アナレンデアフィジーク1905年
アルバート・アインシュタイン (1879-1955)	一般相対性理論: 時空の曲率	1915年	アインシュタイン A.プロイシッシェンアカデミーに関する情報1915年
アーサー・エディントン (1882-1944)	光の偏向の観察 > 時間的曲率の検証	1919年	エディントン A.、ソブラルおよびプリンシペの遠征、1919 年
ハーフェレ＆キーティング	原子時計による時間の遅れの実験測定	1971年	ハーフェレ J.、キーティング R.、科学1972年