The Geometry of Time: Exploring the Fourth Dimension of the Universe

Notion of Time

Since the beginning of the 20th century, the notion of time has ceased to be a simple universal parameter, present since always, to become a dimension integrated into the very structure of the Universe. The theory of special relativity, formulated in 1905 by Albert Einstein (1879-1955), showed that the measured duration depends on the relative motion of the observer. In 1915, general relativity introduced the curvature of spacetime (four-dimensional structure combining space and time) under the effect of mass and energy.

Time and Space United: A Geometric Unity

Spacetime (set of three spatial dimensions and time, forming a four-dimensional manifold) can be described as a four-dimensional manifold where events have coordinates \((x, y, z, ct)\). The Minkowski metric, which formalizes the spacetime interval of special relativity, was formulated in 1908 by Hermann Minkowski (1864-1909).
It defines the invariant interval: $$ \boxed{\color{blue}{\displaystyle s^2}} = (ct)^2 - x^2 - y^2 - z^2 $$
This relation shows that time and space are intimately linked, and that the geometry of time depends on the observer's speed as well as gravitation.

Why Link c and t in Spacetime Coordinates?

The coordinates of an event are often written as (x, y, z, ct) rather than (x, y, z, t) so that the temporal component ct has the same dimension (length) as the spatial coordinates.
Problem: x, y, and z are expressed in meters, while ���� is expressed in seconds → Impossible to add them directly in a norm or distance.
Solution: Multiply ���� by ���� (speed of light), which has the unit m/s: ��������[m]. Thus, ct is in meters, like x, y, z. This homogeneity makes the Minkowski interval, \( \boldsymbol{s^2} = (ct)^2 - x^2 - y^2 - z^2 \), more compact and allows representing space and time in the same four-dimensional geometric framework.

The Minkowski Metric and Spacetime

Type of Spacetime Interval

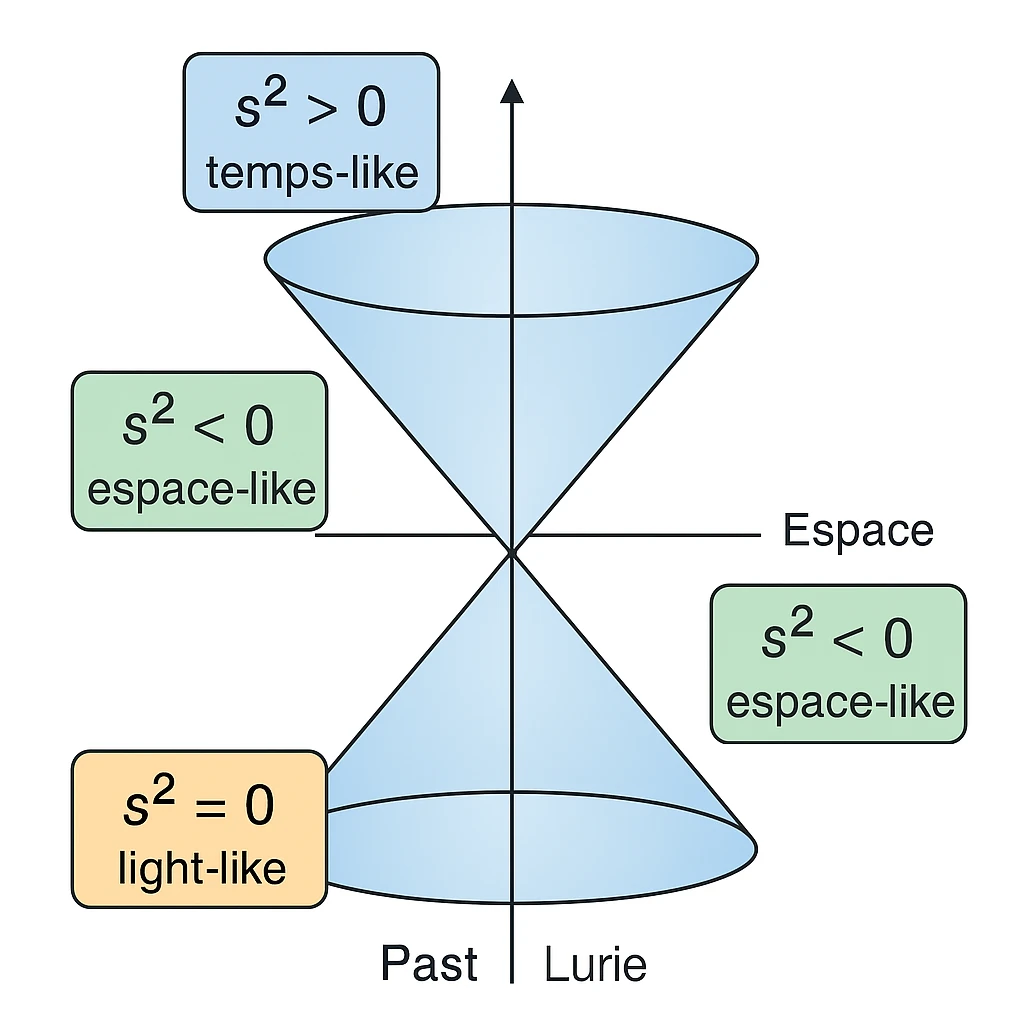
The relation \( s^2 = c^2 t^2 - x^2 - y^2 - z^2 \) is known as the Minkowski metric. It defines an invariant interval (four-dimensional distance between two events in spacetime) between two events in spacetime (combination of three spatial dimensions and time).

Here, \(c\) represents the speed of light, \(t\) the time measured by an observer at rest, and \((x, y, z)\) the spatial coordinates of the events. The invariance of \(s^2\) implies that all observers, regardless of their relative motion or position, will measure the same four-dimensional interval between two events.

This metric shows that time and space are not separate entities: a change in spatial coordinates results in an effective change in perceived time, a phenomenon known as time dilation (time dilation due to relative motion or gravitation). For example, an observer in rapid motion will measure a longer time \(\Delta t\) between two events than an observer at rest.

This mathematical formalization forms the basis of all modern experiments on relativity, whether it be atomic clocks in motion or GPS systems requiring correction of relativistic effects.

Physical Consequences

The time dilation observed for fast particles, or the temporal slowdown near a massive object, confirms that the fourth dimension is not just an abstract concept but a measurable physical property. Experiments conducted with atomic clocks in flight or in orbit demonstrate the validity of relativistic equations with a precision >10^-15.

Summary Table

• Sources: Albert Einstein Archives (new window), Nature (new window), Science (new window).