Journey into the Heart of Paradoxes: The Enigmas That Revolutionized Science

Paradoxes in Physics

Physics is filled with situations where intuition and logic seem to contradict each other. These situations are called paradoxes and have often pushed the boundaries of our scientific understanding, such as the Olbers' paradox, the faint young Sun paradox, Maxwell's demon, the Fermi paradox, Zeno's paradox, the Mpemba effect, the tea leaf paradox, the twin paradox, Schrödinger's cat, wave-particle duality, or the grandfather paradox.

Olbers' Paradox

Cosmological Problem

Olbers' paradox or the dark night sky paradox attempts to answer the question "Why is the night sky dark?" Each of us might simply admit that the cause of the dark night is the absence of the Sun above the horizon, but this is not a good answer. Obviously, the night has always been dark. But if the universe were infinite in space and time, no matter which direction we look, our line of sight should cross a star, even a very distant one. The sky should therefore appear as bright as the Sun everywhere. Yet we observe that the night is essentially dark! To resolve this dark night paradox, we had to completely revise our conception of the Universe.

Resolution of the Paradox

Behind the story of Olbers' paradox lay a troubling cosmic reality from which several concepts emerged at the end of the 20th century.
- The Universe has not always existed; it has a history and a finite age.
- The speed of light is a limiting speed, and the observable Universe can be measured.
- Stars have a finite age and thus a limited lifespan. Their light source is therefore ephemeral.
- The observable Universe is in accelerated expansion. The sky is getting darker because the light from distant galaxies is increasingly redshifted (Doppler effect).

All these hypotheses must be combined to resolve the dark night paradox!

The Faint Young Sun Paradox

Climatic Dilemma

How was a climate suitable for life requiring liquid water maintained on Earth despite the weak sunlight of the young Sun? At the beginning of the creation of the solar system 4.7 billion years ago, the young Sun had only a low luminosity linked to weaker thermonuclear reactions (∼70% of its current luminosity). Such luminosity is insufficient to maintain a liquid ocean on the surface of the young Earth, which should have been completely frozen. Yet, geological data show a warm Earth surface with liquid water and bacterial life from the beginning of Earth's formation. It seems that Earth at that time was already covered with liquid water despite the weak sunlight of the young Sun. What allowed Earth to maintain its water in liquid form? Several explanations, difficult to confirm, have been proposed.

Explanatory Hypotheses

- The greenhouse effect due to a high atmospheric concentration of CO2 produced by intense volcanism allowed Earth to retain its heat.
- Earth's albedo was lower; it reflected less heat into space because its surface was mainly covered by oceans.
- The release of geothermal energy from the heat of radioactive isotope decay may have allowed the young Earth to form natural nuclear fission reactors.
- The Moon was much closer to Earth during its genesis and may have produced significant tidal effects that increased Earth's heat.
- The Sun lost mass; a greater initial mass of the Sun would have compensated for lower irradiance.

The mystery persists!

Maxwell's Demon

Thought Experiment

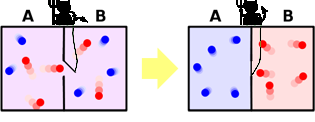
James Clerk Maxwell imagines a box containing a gas, divided into two compartments (A and B) separated by a door at the molecular scale. The demon controls the opening and closing of the door based on the speed of the molecules. The demon allows slower (and thus colder) molecules than the average speed of compartment A to pass from compartment B to A, and allows faster (and thus hotter) molecules than the average speed in B to pass from A to B.

Thermodynamic Consequences

In this thought experiment, the temperature in B increases while that in A decreases. Maxwell's demon thus proposes a process to return to a state of unequal temperature without expending energy, which contradicts the second law of thermodynamics, stating that the entropy of a system can only increase. Here, the total entropy of the system is reduced. For 150 years, this paradox has sparked numerous studies and debates!

The Fermi Paradox

Astronomical Observation

Among the 100 billion star systems in the Milky Way, there are probably many Earth-like planets. The question posed in 1950 by Enrico Fermi (1901-1954) during an informal conversation arises from this observation. Where are they? In other words, if there were technologically advanced extraterrestrial civilizations, their representatives should already be here. Why has no scientific evidence been detected since the advent of technology (no probes, no spacecraft, no radio transmissions, no traces)? The Hubble Space Telescope's ultra-deep field image (shown here) covers one-tenth the diameter of the Moon. In this tiny area, there are about 10,000 galaxies. There would therefore be about 200 billion galaxies in our observable Universe. The presence of planets around a star is relatively common. And if there were only one planet around each star in the universe, the number of planets would be unimaginable.

Analysis and Implications

It would be surprising if nature, structured in the same way throughout the universe, at all scales, had only found the path to life on our planet. The tenacity of life that we observe on Earth is not proof that it is present everywhere in the Universe, patiently waiting for a favorable context to continue its evolution. Yet, it took the birth of a universe, the merging of galaxies, the death of stars to generate all the chemical elements, and the stabilization of a stellar system in a protected zone of a galaxy for intelligent life to appear on a planet, ours, 13.61 billion years after the birth of the Milky Way. And we are far from having reached the technological level allowing us to travel through the Galaxy! Since it practically takes 14 billion years for a civilization capable of leaving its planet to appear, we could conclude that there is no paradox: we are alone because we are the first. "Where are they?" remains, for now, a paradox!

Zeno's Paradox

Achilles and the Tortoise

In the paradox of Achilles and the tortoise, the Greek hero Achilles, known as a very fast runner, races a tortoise. Achilles graciously gives the tortoise a 100-meter head start. Zeno of Elea (490-430 BC) then claims that the swift Achilles can never catch up to the tortoise. Indeed, after a certain time, Achilles will have covered his 100-meter deficit and reached the tortoise's starting point. But during this time, the tortoise will have moved a certain distance, albeit much shorter, say 1 meter. This requires Achilles to take additional time to cover 1 meter, during which the tortoise moves another 1 cm.

Modern Resolution

This requires Achilles to take additional time to cover 1 cm, during which the tortoise will have moved again. Thus, every time Achilles reaches the point where the tortoise was, the tortoise has moved a little further. Consequently, the swift Achilles can never catch up to the tortoise. In a complex modern analysis, the paradox is resolved by the fact that an infinite sum of strictly positive numbers can converge to a finite result!

The Mpemba Effect

Experimental Observation

Erasto Mpemba (1950-), a Tanzanian scientist, was still a high school student when he observed, during cooking classes, that his hot milk placed in the freezer turned into ice cream faster than the same cold preparation. With the help of his physics teacher in Dar es Salaam (Tanzania), he published the data from experiments on the subject in 1969. Experiments conducted over nearly 30 years have shown that hot water can cool faster than cold water.

Conditions of the Phenomenon

This effect is not observed systematically but only under specific conditions. It is a paradoxical phenomenon because, under certain conditions, hot water freezes faster than cold water without us fully understanding why!

The Tea Leaf Paradox

Observation

The tea leaf paradox is a physical phenomenon that is easily observable, where tea leaves in infusion move towards the center rather than the edges of the cup. Indeed, after stirring the tea with a teaspoon, although a centrifugal force proportional to the rotation speed is created, we observe that the tea leaves are attracted to the center of the cup, whereas we would expect them to stay pressed against the edges. The solution was provided by Albert Einstein (1879-1955) in a 1926 article on the cause of river meanders. The rotating liquid in contact with the walls experiences a frictional force. This frictional force tends to slow down the angular rotation speed generated by the centrifugal force.

Physical Explanation

Thus, the liquid at the center will rotate faster and be more strongly attracted outward than the slower-rotating liquid at the edges. The two volumes of tea (fast and slow) will exchange positions. The faster volume will end up at the edges, and the slower volume will migrate towards the center. Initially, the tea leaves are pushed towards the edges and then return to the center, as seen in the video. The tea leaves immersed in the slower tea volume will follow the secondary circulation and end up at the center of the cup. If the tea leaves naturally go to the bottom of the cup, it is because their density is greater than that of the tea.

The Twin Paradox

Statement

The twin paradox arises from a thought experiment that seems to show that special relativity by Albert Einstein is contradictory. The concept of spacetime in special relativity is highly complex; it is only outlined here (without spacetime diagrams). One of the twins makes a round-trip journey into space at a speed close to that of light. When they meet again, the twin who traveled is younger than the twin who stayed on Earth. According to special relativity, measured durations are relative; they depend on the reference frame in which they were measured. There is no absolute present; each reference frame has its own proper time. This is a counterintuitive idea, but the simultaneity of events, due to the speed of light, does not exist. Thus, for the twin in the Earth's reference frame, time passes at the speed measured by their clock. The same is true for the twin in the rocket's reference frame, but the clocks will desynchronize. The clock of the traveling twin will lag behind the other, and this lag will depend on the speed of the rocket. In other words, "time passes more slowly" in the rocket moving uniformly in a straight line relative to Earth than on Earth moving uniformly in a straight line relative to the rocket. But regardless of the rocket's speed, upon returning to Earth, the two twins are no longer the same age. Yet speed is a relative concept. For the twin on Earth, their reference frame (Earth) is stationary, while they see their twin in the rocket moving away at a certain speed. Conversely, for the twin in the rocket, their reference frame (the rocket) is stationary; it is Earth that is moving away. Thus, from the point of view of the twin on Earth, it is the rocket that is moving; it is the time of the rocket that dilates; it is the clock of the rocket that runs slow; it is therefore their twin in the rocket who "ages more slowly".

Explanation

From the point of view of the twin in the rocket, it is Earth that is moving; it is the time of Earth that dilates, and it is their twin on Earth who "ages more slowly". Since the points of view seem symmetric, why is the twin from the rocket younger than their twin upon returning to Earth? The most common explanation for this paradox is that one of the two clocks had to change its inertial reference frame. Indeed, as long as the rocket remains in its inertial reference frame, from the rocket's point of view, it is indeed the twin on Earth who "ages more slowly". But when the rocket turns around, it breaks the symmetry; it changes reference frames, and at that moment, it is the twin in the rocket who "ages more slowly". The turnaround shifted the point of view (the line of simultaneity). But in special relativity, the simultaneity of events between the two reference frames does not exist; we cannot therefore compare the ages of the two twins. To compare their ages, we must wait until they are reunited to see them from the same point of view, at the same point in spacetime, in the same reference frame, with the same proper time. Then, the greater proper time will be that of the twin who did not change reference frames; they are indeed the older one. Their trajectory in spacetime maximized the proper time of their world line, just as a straight line minimizes distance. The clock shift is a real phenomenon experimentally observed in 1991 by two physicists, Joseph Hafele and Richard Keating, with synchronized atomic clocks traveling in two planes that circled the globe twice. One plane flew eastward and the other westward, while a synchronized atomic clock remained on the ground. Upon arrival, the clocks indeed showed the time difference predicted by the theory (special and general). The twin paradox is no longer a paradox!

Schrödinger's Cat

Thought Experiment

Some quantum events only occur because they are observed; if there were no one to see them, they would not exist. This is the very meaning of the "Schrödinger's cat" experiment. In 1935, Erwin Schrödinger (1887-1961) imagined a thought experiment with a real-world cat locked in a box. In this box, a device kills the animal as soon as it detects the decay of a radioactive isotope from the quantum world. In the quantum world, a radioactive atom can exist in two superimposed states, for example, intact and decayed. Quantum mechanics states that as long as the observation is not made, the atom is simultaneously in two states, for example, intact and decayed. But the diabolical mechanism links the state of the cat to the state of the radioactive particle. In other words, the cat is simultaneously dead and alive until the box is opened.

Quantum Interpretation

Since observation triggers the choice between the two states, we cannot say whether the cat is dead or alive before opening the box. Our brain is not ready to accept such a situation for a macroscopic object, and that is where the paradox lies! This state of superposition does not exist in the real world. The major problem is that quantum physics admits superimposed states, completely unknown at the macroscopic level described by classical physics. The explanation is provided by the theory of quantum decoherence. Objects of classical physics (cars, cats, etc.), although composed of atoms described by quantum physics, interact with their environment, with billions of other atoms. These interactions cause the rapid disappearance of superimposed states.

Wave-Particle Duality

Experimental Observation

The world of the extremely small, that of particles (electron, photon, proton, atom, etc.), is not accessible to our senses, including the brain. No image or interpretation can represent the reality of the quantum world; even the words of our language are approximate to describe quantum phenomena. In quantum mechanics, it seems that a particle is both a corpuscle and a wave. This is not the only oddity of quantum physics, but the others (quantum superposition, quantum entanglement, or non-locality) derive from it. What this assertion tells us is that any elementary particle can be seen as a concrete solid body but also as a wave, which is an abstract concept. There is a paradox here! The state of a particle describes all the knowledge (speed, angular momentum, position, energy, etc.) that we can obtain about the particle if we perform experimental measurements on it. Let's look at what the famous experiment called Young's double-slit experiment tells us (see the video here, which describes this experiment in a modern way).

Young's Double-Slit Experiment

1 - When corpuscles (solids) are sent onto a wall with two slits, each corpuscle passes through one slit or the other, bounces in all directions, and impact points mark the screen somewhat randomly behind the slits.
2 - When a wave is sent onto the same wall, the wave passes through both slits, and passing through the slits creates two small waves that will overlap; in some places, they add up, and in others, they cancel out, creating interference fringes on the screen.
3 - When a quantum object is sent, it passes through both slits, interferes like a wave, but when it hits the screen, it suddenly reduces to a point, preferably where the two small waves add up. After a large number of trials, both impacts like corpuscles and interference fringes like waves appear.
4 - But if an observer is added to see which slit the particle passes through, the wave now reduces to a corpuscle at the slits and passes through only one slit at a time. Impact points, not interferences, are then measured on the screen.

The observer modified the experiment by their presence!

The Grandfather Paradox

Statement

Can we travel through time? Special relativity theoretically allows travel into the future; science fiction authors have not hesitated to explore this. The twin paradox is an illustration of this journey into the future. The grandfather paradox is a temporal paradox that forbids travel into the past. Why is it a paradox? If a time traveler projects themselves into the past, they could kill their grandfather before he has children. And here we understand the paradox: our traveler would never have been born, would never have been able to return to the past, and would never have been able to kill their grandfather!!!

Reason for the Paradox

One cannot both be born and not be born. In physics, the principle of causality cannot be violated. A cause always precedes its effects, and an effect can never retroact on its cause. In other words, no effect can precede its cause. The grandfather paradox seems to appear for the first time in this exact form in a science fiction novel by René Barjavel (1911-1985), Le Voyageur imprudent, in 1944.