Chaostheorie und der Schmetterlingseffekt

Bildbeschreibung:Seltsamer Attraktorvom Meteorologen Edward Lorenz (1917-2008). Die mathematische Darstellung eines dynamischen Systems in einem Computer zeigt eine Figur namens „Attraktor“, die die Bewegungen eines Objekts, also seine Geschwindigkeit und seine Position, getreu wiedergibt. Es war Edward Lorenz, der zufällig das Grundprinzip der Chaostheorie entdeckte. Indem er die Anfangsbedingungen eines Computer-Wettervorhersagesystems ändert, zeigt er, dass eine geringe anfängliche Unsicherheit zu einer zunehmenden Unsicherheit in der Vorhersage führt. Diese Unsicherheit wird nach langer Zeit inakzeptabel. Er kommt zu dem Schluss, dass diese Sensibilität gegenüber Anfangsbedingungen dazu führt, dass man jegliche Hoffnung auf langfristige Vorhersagen verliert, was wir den Lorenz-Schmetterlingseffekt nennen. Mit anderen Worten: Der Flügelschlag eines Schmetterlings kann Tausende von Kilometern entfernt verheerende Hurrikane auslösen. Bildquelle: Public Domain.

Zufall und Chaos

Die Welt um uns herum erscheint unvorhersehbar, ungeordnet, gefährlich und chaotisch. Ein chaotisches System ist ein einfaches oder komplexes System,empfindlich gegenüber Anfangsbedingungenund die einen sich wiederholenden Charakter oder eine starke Wiederholung aufweist.

Eine kleine Störung kann zu einer gigantischen Instabilität oder einem Ungleichgewicht führen, das auf lange Sicht nicht vorhersehbar ist. So können einfache Geräte komplexe Phänomene hervorrufen.

Ein chaotisches System ist das Gegenteil eines vollkommen regulären Systems. In der Himmelsmechanik schienen die Bewegungen der Planeten um die Sonne lange Zeit einem regelmäßigen System zuzugehören.

Seit der großen astronomischen Revolution vertrat Nikolaus Kopernikus (1473-1543) die einfache Idee, dass sich die Planeten um die Sonne drehen. Johannes Kepler (1571-1630) konnte dann mit großer Präzision die Bahnen der Planeten um die Sonne berechnen.

Dann erklärte Isaac Newton (1642-1727) alle Himmelsbewegungen mit einem einzigen und einfachen Gesetz, dem Gesetz der Gravitation. Materie zieht Materie entsprechend der vorhandenen Massen an und umgekehrt proportional zum Quadrat ihrer Entfernung. Dies ermöglicht präzise Berechnungen und vor allem Prognosen. Mit diesem einfachen Gesetz erklären wir alle Himmelsbewegungen.

Allerdings bestehen Diskrepanzen zwischen astronomischen Beobachtungen und Berechnungen und dennoch sind die mathematischen Gesetze der Gravitationstheorie exakt. Dies liegt daran, dass die Gesetze in einem System mit zwei Himmelsobjekten perfekt funktionieren, im Universum jedoch alle Himmelsobjekte dem Gravitationseinfluss anderer unterliegen.

Es sind diese kleinen Schwankungen, diese Turbulenzen, diese Gravitationsstörungen, die letztendlich zur Instabilität des Systems führen. Die Chaostheorie entstand in den 1970er Jahren mit der Informatik. Die Informatik ermöglichte die unmittelbare Visualisierung der Komplexität dynamischer Systeme wie des Sonnensystems. Es ist genau die Untersuchung der Bewegung dreier Körper in gravitativer Wechselwirkung, wie der Sonne, der Erde und des Mondes, die den Ursprung der Chaostheorie bildet.

Das Dreikörpersystem

Die Untersuchung des Problems der drei vom Rest des Universums isolierten Körper hat es ermöglicht, die Stabilität des Sonnensystems auf lange Sicht zu ermitteln. Die Wissenschaftler wollten wissen, wie hoch das Risiko ist, dass einer der Körper mit einem anderen kollidiert, oder wie hoch das Risiko ist, dass einer der Körper aus dem Sonnensystem geschleudert wird. Pierre-Simon Laplace (1749–1827) glaubte an die Stabilität des Systems, doch der französische Mathematiker Henri Poincaré (1854–1912) entdeckte ein Jahrhundert später das potenzielle Chaos, das in den Gleichungen der Theorie dynamischer Systeme verborgen war.

Poincaré vereinfacht die Berechnungen, indem er ein Sonnensystem untersucht, das nur drei Körper enthält: Erde, Mond, Sonne. Dann versteht er, dass es unmöglich ist, ihre Wechselwirkungen zu berechnen und ihre Flugbahnen über einen langen Zeitraum zu bestimmen, weil dieses Minisystem, das durch die Gleichungen perfekt beschrieben wird, unvorhersehbar ist. Sein Beitrag zum Dreikörperproblem machte ihn zum Vorläufer der Chaostheorie, da er eine Vielzahl von Konzepten einführte.

Mathematische Darstellung

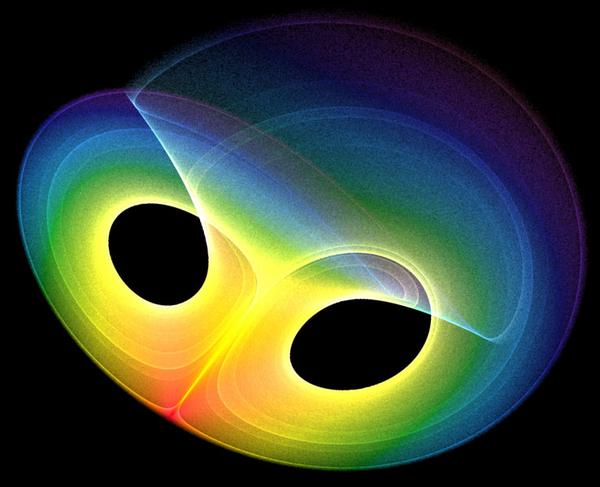
Derzeit zeigt die mathematische Darstellung eines dynamischen Systems in einem Computer eine Figur (siehe Bild), die als „Attraktor“ bezeichnet wird und die Bewegung des Systems getreu wiedergibt. Dieser Attraktor erklärt die Regelmäßigkeit der Bewegung, also ihre Geschwindigkeit und ihre Position. Ein vollkommen regelmäßiges System wird durch einen sehr einfachen Attraktor dargestellt, beispielsweise einen Kreis oder eine Ellipse.

Wenn eine Störung das System leicht zu einer Veränderung zwingt, kann es instabil werden und der Attraktor zeigt ein chaotisches und unvorhersehbares Muster. Bewegungen, die auf mathematische Gesetze reagieren und unvorhersehbar bleiben, werden von Wissenschaftlern „Chaos“ genannt.

Seitdem haben Wissenschaftler herausgefunden, dass die Chaostheorie auf fast alle dynamischen Systeme und in vielen Bereichen wie Strömungsmechanik, Wirtschaftswissenschaften, Funkübertragung oder Wettervorhersage anwendbar ist.

Abschluss

Die Umlaufbahn der Planeten wird auf lange Sicht chaotisch und es treten Chaoserscheinungen auf, da sie sehr empfindlich auf die Anfangsbedingungen reagieren. Ein sehr kleiner Fehler von 15 Metern in der Anfangsposition der Erde auf ihrer Umlaufbahn kann sich nach 100 Millionen Jahren in einen Fehler von 150 Millionen Kilometern verwandeln, das heißt, die Erde kann sich irgendwo im Sonnensystem befinden, 300 Millionen Kilometer von der Sonne entfernt oder von ihr absorbiert werden. Das Gleiche gilt für die Umlaufbahn des Merkur, der nach längerer Zeit völlig abflachen und bis zur Venus reichen kann. Die Chaostheorie zeigt die Instabilität des Sonnensystems und lehrt uns, dass wir nicht alles berechnen können. Der Zufall hat Einzug in unsere wissenschaftliche Beschreibung der Welt gehalten und dank der Chaostheorie ist ein Teil dieser Unsicherheit nun verständlich. Wir können somit die qualitativen Eigenschaften dynamischer Systeme interpretieren und erhalten dadurch eine Vorstellung von ihrem Verhalten, ohne sie genau zu berechnen. Alles wird durch eine zufällige Abfolge von Ursachen und dann Wirkungen erklärt, jedes Ereignis wird durch ein Kausalitätsprinzip bestimmt. Das gesamte Universum ist deterministisch, aber es wird „Chaos“ entstehen.