Teoría del Caos y Efecto Mariposa

Descripción de la imagen: Atractor Extraño del meteorólogo Edward Lorenz (1917-2008). La representación matemática de un sistema dinámico en una computadora muestra una figura llamada "atractor" que traduce fielmente los movimientos de un objeto, es decir, su velocidad y posición. Fue Edward Lorenz quien descubrió por casualidad el principio fundador de la teoría del caos. Al modificar las condiciones iniciales de un sistema informático de predicción meteorológica, demostró que una pequeña incertidumbre inicial da lugar a una incertidumbre creciente en las predicciones. Esta incertidumbre se vuelve inaceptable después de un tiempo largo. Concluyó que esta sensibilidad a las condiciones iniciales hace perder toda esperanza de predicción a largo plazo, lo que se conoce como el efecto mariposa de Lorenz. En otras palabras, el aleteo de una mariposa puede desencadenar huracanes devastadores a miles de kilómetros de distancia. Fuente de la imagen: dominio público.

Azar y Caos

El mundo que nos rodea parece impredecible, desordenado, aleatorio y caótico. Un sistema caótico es un sistema simple o complejo, sensible a las condiciones iniciales, y que presenta un carácter repetitivo o una fuerte recurrencia.

Una pequeña perturbación puede provocar una inestabilidad o un desequilibrio gigantesco impredecible a largo plazo. Así, los dispositivos simples pueden dar lugar a fenómenos complejos.

Un sistema caótico es lo contrario de un sistema perfectamente regular. En mecánica celeste, los movimientos de los planetas alrededor del Sol han parecido durante mucho tiempo pertenecer a un sistema regular.

Desde la gran revolución astronómica, Nicolás Copérnico (1473-1543) impuso la idea simple de que los planetas giran alrededor del Sol. Johannes Kepler (1571-1630) pudo entonces calcular, con gran precisión, las trayectorias de los planetas alrededor del Sol.

Luego, Isaac Newton (1642-1727) explicó todos los movimientos celestes con una sola y simple ley, la ley de la gravitación. La materia atrae a la materia en función de las masas presentes e inversamente al cuadrado de su distancia. Esto permite realizar cálculos precisos y, sobre todo, predicciones. Con esta simple ley se explican todos los movimientos celestes.

Sin embargo, existen desviaciones entre las observaciones astronómicas y los cálculos, y sin embargo las leyes matemáticas de la teoría de la gravitación son exactas. Esto se debe a que las leyes funcionan perfectamente en un sistema de dos objetos celestes, pero en el universo todos los objetos celestes están sujetos a la influencia gravitacional de los demás.

Son estas pequeñas fluctuaciones, estas turbulencias, estas perturbaciones gravitacionales las que finalmente fuerzan la inestabilidad del sistema. La teoría del caos surgió con la informática en la década de 1970. La informática permitió la visualización inmediata de la complejidad de los sistemas dinámicos como el sistema solar. Es precisamente el estudio del movimiento de tres cuerpos en interacción gravitacional, como el del Sol, la Tierra y la Luna, lo que dio origen a la teoría del caos.

El Sistema de Tres Cuerpos

El estudio del problema de los 3 cuerpos aislados del resto del universo permitió conocer la estabilidad del sistema solar a largo plazo. Los científicos querían conocer los riesgos de colisión de uno de los cuerpos con otro o los riesgos de que uno de los cuerpos fuera expulsado del Sistema Solar. Pierre-Simon Laplace (1749-1827) creía en la estabilidad del sistema, pero el matemático francés Henri Poincaré (1854-1912), un siglo más tarde, descubrió el caos potencial oculto en las ecuaciones de la teoría de los sistemas dinámicos.

Poincaré simplificó los cálculos estudiando un sistema solar que contenía solo tres cuerpos: Tierra, Luna y Sol. Entonces comprendió que es imposible calcular sus interacciones y determinar sus trayectorias durante un largo período porque este mini sistema, perfectamente descrito por las ecuaciones, es impredecible. Su contribución al problema de los tres cuerpos lo convierte en un precursor de la teoría del caos, ya que introdujo muchos conceptos.

Representación Matemática

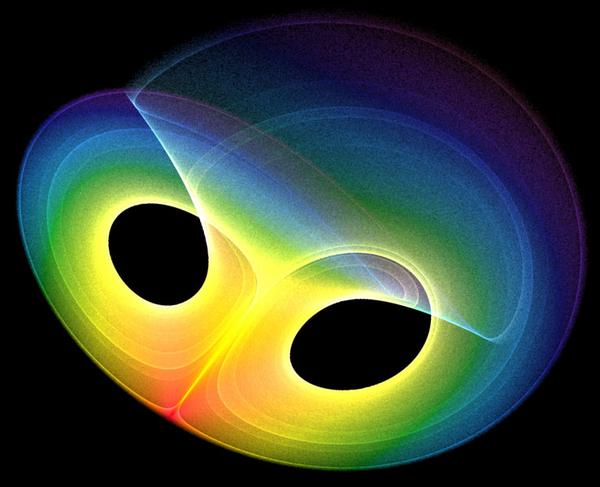
Actualmente, la representación matemática de un sistema dinámico en una computadora muestra una figura (ver imagen) llamada "atractor" que traduce fielmente el movimiento del sistema. Este atractor da cuenta de la regularidad del movimiento, es decir, su velocidad y posición. Un sistema perfectamente regular será representado por un atractor muy simple, como un círculo o una elipse.

Cuando una perturbación fuerza ligeramente al sistema a cambiar, puede volverse inestable y el atractor muestra una figura caótica e impredecible. Los movimientos que responden a leyes matemáticas y que permanecen impredecibles son llamados "Caos" por los científicos.

Desde entonces, los científicos han descubierto que la teoría del caos se aplica a casi todos los sistemas dinámicos y en muchos campos como la mecánica de fluidos, la economía, las transmisiones de radio o la previsión meteorológica.

Conclusión

La órbita de los planetas se vuelve caótica a largo plazo y las manifestaciones del caos aparecen ya que son muy sensibles a las condiciones iniciales. Un pequeño error de 15 metros en la posición inicial de la Tierra en su órbita puede, después de 100 millones de años, convertirse en un error de 150 millones de km, es decir, la Tierra puede terminar en cualquier lugar del sistema solar, a 300 millones de km del Sol o absorbida por él. Lo mismo ocurre con la órbita de Mercurio, que después de un largo tiempo puede aplanarse completamente e ir hasta Venus. La teoría del caos muestra la inestabilidad del sistema solar y nos enseña que no podemos calcularlo todo. El azar se ha introducido en nuestra descripción científica del mundo y, gracias a la teoría del caos, parte de esta incertidumbre es ahora comprensible. Podemos así interpretar las propiedades cualitativas de los sistemas dinámicos y hacernos una idea de sus comportamientos sin calcularlos exactamente. Todo se explica por una cadena aleatoria de causas y efectos; cada evento está determinado por un principio de causalidad. Todo el universo es determinista, pero emergerá un "caos".