Théorie du Chaos et Effet Papillon

Description de l'image : Attracteur Etrange du météorologue Edward Lorenz (1917-2008). La représentation mathématique d'un système dynamique dans un ordinateur montre une figure appelée un "attracteur" qui traduit fidèlement les mouvements d'un objet c'est-à-dire sa vitesse et sa position. C'est Edward Lorenz qui par hasard découvre le principe fondateur de la théorie du chaos. En modifiant les conditions initiales d'un système informatique de prévision météorologique, il démontre qu'une faible incertitude initiale donne lieu à une incertitude croissante dans les prévisions. Cette incertitude devient inacceptable après un temps long. Il en conclut que cette sensibilité aux conditions initiales faire perdre tout espoir de prévision à long terme, c'est ce que l'on appelle l'effet papillon de Lorenz. Autrement dit, le battement d'ailes d'un papillon peut déclencher des ouragans dévastateurs des milliers de kilomètres plus loin. Source image : domaine public.

Hasard et Chaos

Le monde qui nous entoure parait imprévisible, désordonné, hasardeux et chaotique. Un système chaotique est un système simple ou complexe, sensible aux conditions initiales et qui présente un caractère répétitif ou une forte récurrence.

Une petite perturbation peut entrainer une instabilité ou un déséquilibre gigantesque non prédictible à long terme. Ainsi les dispositifs simples peuvent donner lieu à des phénomènes complexes.

Un système chaotique est l'inverse d'un système parfaitement régulier. En mécanique céleste, les mouvements des planètes autour du Soleil ont longtemps semblés appartenir à un système régulier.

Depuis la grande révolution astronomique, Nicolas Copernic (1473-1543) impose l'idée simple que les planètes tournent autour du Soleil. Johannes Kepler (1571-1630) peut alors calculer, avec une grande précision, les trajectoires des planètes autour du Soleil.

Puis Isaac Newton (1642-1727) explique tous les mouvements célestes avec une seule et simple loi, la loi de la gravitation. La matière attire la matière en fonction des masses en présence, et inversement au carré de leur distance. Cela permet de faire des calculs précis et surtout des prévisions. Avec cette simple loi on explique tous les mouvements célestes.

Cependant des décalages existent entre les observations astronomiques et les calculs et pourtant les lois mathématiques de la théorie de la gravitation sont exactes. Cela vient du fait que les lois fonctionnent parfaitement dans un système à deux objets célestes, mais dans l'univers tous les objets célestes subissent l'influence gravitationnelle des autres.

Ce sont ces petites fluctuations, ces turbulences, ces perturbations gravitationnelles qui finissent par forcer l'instabilité du système. La théorie du chaos a émergé avec l'informatique dans les années 1970. L'informatique a permis la visualisation immédiate de la complexité des systèmes dynamiques comme le système solaire. C'est justement l'étude du mouvement de trois corps en interaction gravitationnelle, comme celui du Soleil, de la Terre et de la Lune, qui est à l'origine de la théorie du chaos.

Le Système à trois corps

L'étude du problème des 3 corps isolés du reste de l'univers a permis de connaitre la stabilité du système solaire sur le long terme. Les scientifiques voulaient connaitre les risques de collision d'un des corps avec un autre ou les risques d'un des corps d'être éjecté du Système solaire. Pierre-Simon Laplace (1749-1827) croyait en la stabilité du système mais le mathématicien français Henri Poincaré (1854-1912), un siècle plus tard, découvre le chaos potentiel caché dans les équations de la théorie des systèmes dynamiques.

Poincaré simplifie les calculs en étudiant un système solaire contenant seulement trois corps, Terre, Lune, Soleil. Il comprend alors qu'il est impossible de calculer leur interactions et de déterminer leurs trajectoires sur un temps long car ce mini système, parfaitement décrit par les équations, est imprévisible. Sa contribution au problème des trois corps en fait le précurseur de la théorie du chaos car il a introduit un grand nombre de concepts.

Représentation mathématique

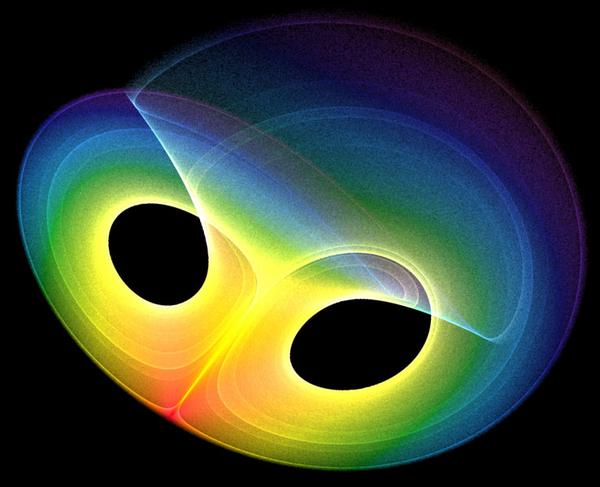
Actuellement, la représentation mathématique d'un système dynamique dans un ordinateur, montre une figure (voir image) appelée un "attracteur" qui traduit fidèlement le mouvement du système. Cette attracteur rend compte de la régularité du mouvement c'est-à-dire sa vitesse et sa position. Un système parfaitement régulier sera représenté par un attracteur très simple, tel un cercle ou une ellipse.

Lorsque qu'une perturbation force légèrement le système à changer, il peut devenir instable et l'attracteur montre une figure chaotique et imprévisible. Les mouvements qui répondent à des lois mathématiques et qui restent imprévisibles sont appelés par les scientifiques "Chaos".

Depuis les scientifiques ont découvert que la théorie du chaos s'applique à presque tous les systèmes dynamiques et dans de nombreux domaines comme la mécanique des fluides, l'économie, les transmissions radio ou la prévision météorologique.

Conclusion

L'orbite des planètes devient à long terme chaotique et les manifestations du chaos apparaissent puisqu'elles sont très sensibles aux conditions initiales. Une toute petite erreur de 15 mètres sur la position initiale de la Terre sur son orbite, peut au bout de 100 millions d'années se transformer en une erreur de 150 millions de km, c'est-à-dire que la Terre peut se retrouver n'importe où dans le système solaire, à 300 millions de km du Soleil ou absorbée par lui. Il en est de même pour l'orbite de Mercure qui peut, après un temps long, complètement s'aplatir et aller jusqu'à Vénus. La théorie du chaos montre l'instabilité du système solaire et nous enseigne que l'on ne peut pas tout calculer. Le hasard s'est introduit dans notre description scientifique du monde et grâce à la théorie du chaos, une partie de cette incertitude est maintenant compréhensible. On peut ainsi interpréter les propriétés qualitatives des systèmes dynamiques et cela nous donne une idée de leurs comportements sans les calculer exactement. Tout s'explique par un enchainement aléatoire de causes puis d'effets, chaque évènement est déterminé par un principe de causalité. Tout l'univers est déterministe mais un « chaos » émergera.