Teoria do Caos e Efeito Borboleta

Descrição da imagem: Atractor Estranho do meteorologista Edward Lorenz (1917-2008). A representação matemática de um sistema dinâmico em um computador mostra uma figura chamada "attractor" que traduz fielmente os movimentos de um objeto, ou seja, sua velocidade e posição. Foi Edward Lorenz quem descobriu por acaso o princípio fundador da teoria do caos. Ao modificar as condições iniciais de um sistema de computador de previsão meteorológica, ele demonstrou que uma pequena incerteza inicial leva a uma incerteza crescente nas previsões. Esta incerteza torna-se inaceitável após um longo tempo. Ele concluiu que esta sensibilidade às condições iniciais faz perder toda a esperança de previsão a longo prazo, o que é conhecido como o efeito borboleta de Lorenz. Em outras palavras, o bater de asas de uma borboleta pode desencadear furacões devastadores a milhares de quilômetros de distância. Fonte da imagem: domínio público.

Acaso e Caos

O mundo ao nosso redor parece imprevisível, desordenado, aleatório e caótico. Um sistema caótico é um sistema simples ou complexo, sensível às condições iniciais, e que apresenta um caráter repetitivo ou uma forte recorrência.

Uma pequena perturbação pode levar a uma instabilidade ou desequilíbrio gigantesco imprevisível a longo prazo. Assim, dispositivos simples podem dar origem a fenômenos complexos.

Um sistema caótico é o oposto de um sistema perfeitamente regular. Na mecânica celeste, os movimentos dos planetas em torno do Sol pareciam durante muito tempo pertencer a um sistema regular.

Desde a grande revolução astronômica, Nicolau Copérnico (1473-1543) impôs a ideia simples de que os planetas giram em torno do Sol. Johannes Kepler (1571-1630) pôde então calcular, com grande precisão, as trajetórias dos planetas em torno do Sol.

Em seguida, Isaac Newton (1642-1727) explicou todos os movimentos celestes com uma única e simples lei, a lei da gravitação. A matéria atrai a matéria de acordo com as massas presentes e inversamente ao quadrado de sua distância. Isso permite realizar cálculos precisos e, sobretudo, previsões. Com esta lei simples, todos os movimentos celestes são explicados.

No entanto, existem desvios entre as observações astronômicas e os cálculos, e no entanto as leis matemáticas da teoria da gravitação são exatas. Isso ocorre porque as leis funcionam perfeitamente em um sistema de dois objetos celestes, mas no universo todos os objetos celestes estão sujeitos à influência gravitacional dos outros.

São essas pequenas flutuações, essas turbulências, essas perturbações gravitacionais que acabam forçando a instabilidade do sistema. A teoria do caos surgiu com a informática na década de 1970. A informática permitiu a visualização imediata da complexidade dos sistemas dinâmicos como o sistema solar. É precisamente o estudo do movimento de três corpos em interação gravitacional, como o do Sol, da Terra e da Lua, que deu origem à teoria do caos.

O Sistema de Três Corpos

O estudo do problema dos 3 corpos isolados do resto do universo permitiu conhecer a estabilidade do sistema solar a longo prazo. Os cientistas queriam conhecer os riscos de colisão de um dos corpos com outro ou os riscos de um dos corpos ser ejetado do Sistema Solar. Pierre-Simon Laplace (1749-1827) acreditava na estabilidade do sistema, mas o matemático francês Henri Poincaré (1854-1912), um século depois, descobriu o caos potencial escondido nas equações da teoria dos sistemas dinâmicos.

Poincaré simplificou os cálculos estudando um sistema solar contendo apenas três corpos: Terra, Lua e Sol. Ele então compreendeu que é impossível calcular suas interações e determinar suas trajetórias durante um longo período porque este mini sistema, perfeitamente descrito pelas equações, é imprevisível. Sua contribuição para o problema dos três corpos o torna um precursor da teoria do caos, pois introduziu muitos conceitos.

Representação Matemática

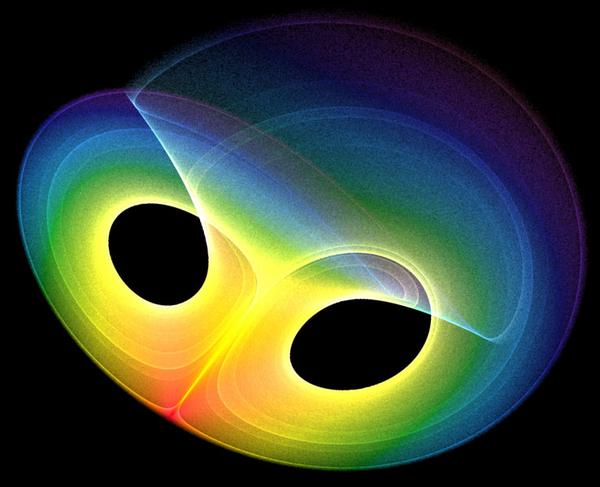
Atualmente, a representação matemática de um sistema dinâmico em um computador mostra uma figura (ver imagem) chamada "attractor" que traduz fielmente o movimento do sistema. Este atractor dá conta da regularidade do movimento, ou seja, sua velocidade e posição. Um sistema perfeitamente regular será representado por um atractor muito simples, como um círculo ou uma elipse.

Quando uma perturbação força ligeiramente o sistema a mudar, ele pode se tornar instável e o atractor mostra uma figura caótica e imprevisível. Os movimentos que respondem a leis matemáticas e que permanecem imprevisíveis são chamados de "Caos" pelos cientistas.

Desde então, os cientistas descobriram que a teoria do caos se aplica a quase todos os sistemas dinâmicos e em muitos campos, como a mecânica dos fluidos, a economia, as transmissões de rádio ou a previsão meteorológica.

Conclusão

A órbita dos planetas torna-se caótica a longo prazo e as manifestações do caos aparecem, pois são muito sensíveis às condições iniciais. Um pequeno erro de 15 metros na posição inicial da Terra em sua órbita pode, após 100 milhões de anos, transformar-se em um erro de 150 milhões de km, ou seja, a Terra pode acabar em qualquer lugar do sistema solar, a 300 milhões de km do Sol ou absorvida por ele. O mesmo acontece com a órbita de Mercúrio, que após um longo tempo pode se achatar completamente e ir até Vênus. A teoria do caos mostra a instabilidade do sistema solar e nos ensina que não podemos calcular tudo. O acaso introduziu-se na nossa descrição científica do mundo e, graças à teoria do caos, parte dessa incerteza é agora compreensível. Podemos assim interpretar as propriedades qualitativas dos sistemas dinâmicos e fazer uma ideia dos seus comportamentos sem os calcular exatamente. Tudo se explica por uma cadeia aleatória de causas e efeitos; cada evento é determinado por um princípio de causalidade. Todo o universo é determinista, mas emergirá um "caos".