Chaos Theory and Butterfly Effect

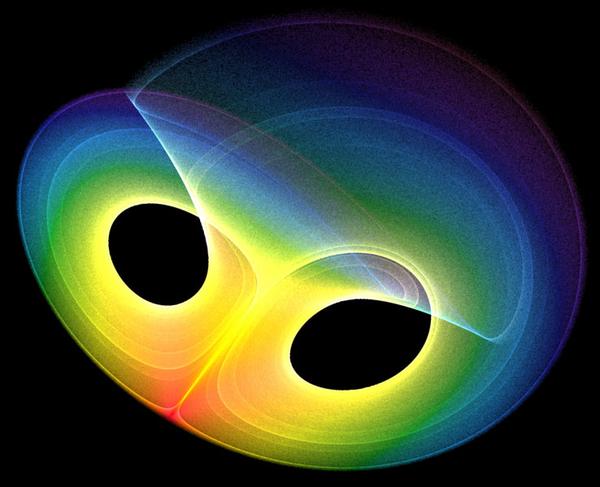
Image description: Strange Attractor by meteorologist Edward Lorenz (1917-2008). The mathematical representation of a dynamic system in a computer shows a figure called an "attractor" that faithfully translates the movements of an object, i.e., its speed and position. It was Edward Lorenz who accidentally discovered the founding principle of chaos theory. By modifying the initial conditions of a computer weather forecasting system, he demonstrated that a small initial uncertainty leads to growing uncertainty in predictions. This uncertainty becomes unacceptable after a long time. He concluded that this sensitivity to initial conditions makes any hope of long-term prediction impossible, which is known as Lorenz's butterfly effect. In other words, the flapping of a butterfly's wings can trigger devastating hurricanes thousands of kilometers away. Image source: public domain.

Chance and Chaos

The world around us seems unpredictable, disorderly, random, and chaotic. A chaotic system is a simple or complex system, sensitive to initial conditions, and exhibits a repetitive or highly recurrent nature.

A small perturbation can lead to gigantic, unpredictable instability or imbalance in the long term. Thus, simple devices can give rise to complex phenomena.

A chaotic system is the opposite of a perfectly regular system. In celestial mechanics, the movements of the planets around the Sun have long seemed to belong to a regular system.

Since the great astronomical revolution, Nicolas Copernicus (1473-1543) imposed the simple idea that the planets revolve around the Sun. Johannes Kepler (1571-1630) could then calculate, with great precision, the trajectories of the planets around the Sun.

Then Isaac Newton (1642-1727) explained all celestial movements with a single, simple law, the law of gravitation. Matter attracts matter according to the masses present, and inversely to the square of their distance. This allows for precise calculations and, above all, predictions. With this simple law, all celestial movements are explained.

However, discrepancies exist between astronomical observations and calculations, yet the mathematical laws of the theory of gravitation are exact. This is because the laws work perfectly in a system of two celestial objects, but in the universe, all celestial objects are subject to the gravitational influence of others.

It is these small fluctuations, these turbulences, these gravitational perturbations that eventually force the instability of the system. Chaos theory emerged with computers in the 1970s. Computers allowed the immediate visualization of the complexity of dynamic systems like the solar system. It is precisely the study of the movement of three bodies in gravitational interaction, such as that of the Sun, Earth, and Moon, that gave rise to chaos theory.

The Three-Body System

The study of the problem of 3 bodies isolated from the rest of the universe allowed us to know the stability of the solar system over the long term. Scientists wanted to know the risks of collision of one of the bodies with another or the risks of one of the bodies being ejected from the Solar System. Pierre-Simon Laplace (1749-1827) believed in the stability of the system, but the French mathematician Henri Poincaré (1854-1912), a century later, discovered the potential chaos hidden in the equations of the theory of dynamic systems.

Poincaré simplified the calculations by studying a solar system containing only three bodies: Earth, Moon, and Sun. He then understood that it is impossible to calculate their interactions and determine their trajectories over a long period because this mini-system, perfectly described by the equations, is unpredictable. His contribution to the three-body problem makes him a precursor of chaos theory, as he introduced many concepts.

Mathematical Representation

Currently, the mathematical representation of a dynamic system in a computer shows a figure (see image) called an "attractor" that faithfully translates the movement of the system. This attractor accounts for the regularity of the movement, i.e., its speed and position. A perfectly regular system will be represented by a very simple attractor, such as a circle or an ellipse.

When a perturbation slightly forces the system to change, it can become unstable, and the attractor shows a chaotic and unpredictable figure. Movements that respond to mathematical laws and remain unpredictable are called "Chaos" by scientists.

Since then, scientists have discovered that chaos theory applies to almost all dynamic systems and in many fields such as fluid mechanics, economics, radio transmissions, or weather forecasting.

Conclusion

The orbit of the planets becomes chaotic in the long term, and the manifestations of chaos appear since they are very sensitive to initial conditions. A tiny error of 15 meters in the initial position of the Earth on its orbit can, after 100 million years, turn into an error of 150 million km, i.e., the Earth can end up anywhere in the solar system, 300 million km from the Sun or absorbed by it. The same applies to the orbit of Mercury, which, after a long time, can completely flatten and go as far as Venus. Chaos theory shows the instability of the solar system and teaches us that we cannot calculate everything. Chance has entered our scientific description of the world, and thanks to chaos theory, part of this uncertainty is now understandable. We can thus interpret the qualitative properties of dynamic systems and get an idea of their behaviors without calculating them exactly. Everything is explained by a random chain of causes and effects; each event is determined by a principle of causality. The entire universe is deterministic, but a "chaos" will emerge.