最終更新日: 2025 年 8 月 29 日

カオス理論とバタフライ効果

チャンスとカオス

私たちの周りの世界は、予測不可能で、無秩序で、危険で、混沌としているように見えます。カオスシステムとは、単純または複雑なシステムのことです。初期条件に敏感反復性または強い再発性を示します。

小さな外乱が、長期的には予測できない巨大な不安定性や不均衡を引き起こす可能性があります。このように、単純なデバイスが複雑な現象を引き起こす可能性があります。

カオスシステムは、完全に規則的なシステムの反対です。天体力学では、太陽の周りの惑星の動きは長い間、規則的なシステムに属していると考えられてきました。

天文学の大革命以来、ニコラ・コペルニクス (1473-1543) は、惑星が太陽の周りを回っているという単純な考えを押し付けました。ヨハネス・ケプラー (1571-1630) は、太陽の周りの惑星の軌道を非常に正確に計算することができました。

その後、アイザックニュートン (1642-1727) は、すべての天体の動きを単一の単純な法則である重力の法則で説明しました。物質は、存在する質量に基づいて、距離の二乗に反比例して物質を引き付けます。これにより、正確な計算、そして何よりも予測が可能になります。この単純な法則で、すべての天体の動きを説明できます。

しかし、天文観測と計算の間には矛盾が存在しますが、それでも重力理論の数学的法則は正確です。これは、2 つの天体を含む系では法則が完全に機能するためですが、宇宙ではすべての天体が他の天体の重力の影響を受けるからです。

これらの小さな変動、乱流、重力の擾乱が、最終的にシステムの不安定性を強いるのです。カオス理論は 1970 年代にコンピューターサイエンスとともに登場しました。コンピューターサイエンスにより、太陽系のような動的システムの複雑さを即座に視覚化できるようになりました。それはまさに、太陽、地球、月のような重力相互作用における 3 つの天体の動きの研究であり、カオス理論の起源です。

三体システム

宇宙の他の部分から隔離された 3 つの天体の問題の研究により、太陽系の長期的な安定性を知ることが可能になりました。科学者たちは、一方の天体が他方の天体に衝突するリスク、あるいは一方の天体が太陽系から弾き出されるリスクを知りたいと考えていました。ピエール＝シモン・ラプラス (1749-1827) はシステムの安定性を信じていましたが、その 1 世紀後、フランスの数学者アンリ・ポアンカレ (1854-1912) は、動的システム理論の方程式に潜在的なカオスが隠れていることを発見しました。

ポアンカレは、地球、月、太陽の 3 つの天体のみを含む太陽系を研究することで計算を簡素化します。そして、方程式で完全に記述されるこのミニシステムは予測不可能であるため、それらの相互作用を計算し、長期にわたってそれらの軌道を決定することは不可能であることを理解しました。三体問題への彼の貢献により、彼は多数の概念を導入したため、カオス理論の先駆者となりました。

数学的表現

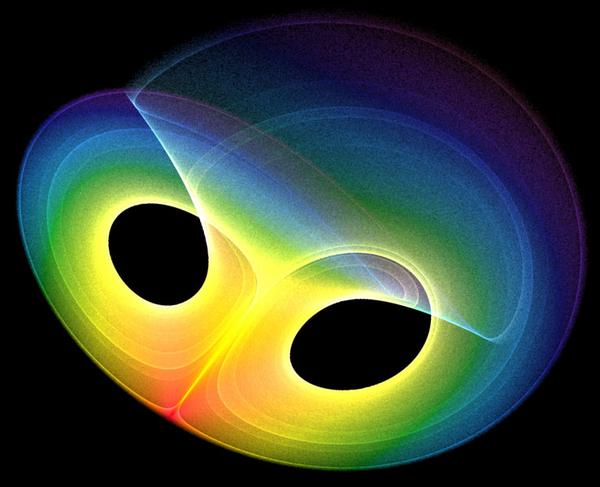
現在、コンピュータにおける動的システムの数学的表現は、システムの動きを忠実に表現する「アトラクター」と呼ばれる図形 (画像を参照) を示しています。このアトラクターは、動きの規則性、つまり速度と位置を説明します。完全に規則的なシステムは、円や楕円などの非常に単純なアトラクターによって表されます。

外乱によってシステムがわずかに強制的に変更されると、システムが不安定になり、アトラクターが混沌とした予測不可能なパターンを示すことがあります。数学的法則に反応し、予測不可能な動きを科学者は「カオス」と呼びます。

それ以来、科学者たちはカオス理論がほぼすべての動的システムに適用され、流体力学、経済学、無線通信、天気予報などの多くの分野に適用できることを発見しました。

結論

惑星の軌道は長期的には無秩序になり、初期条件に非常に敏感であるため、カオスの兆候が現れます。地球の軌道上の初期位置における 15 メートルという非常に小さな誤差は、1 億年後には 1 億 5,000 万 km の誤差に変わる可能性があります。つまり、地球は太陽系内のどこにでも存在する可能性があり、太陽から 3 億 km 離れた場所、または太陽に吸収される可能性があります。水星の軌道も同様で、長い時間が経つと完全に平らになり、金星にまで達する可能性があります。カオス理論は太陽系の不安定性を示し、すべてを計算することはできないことを教えてくれます。世界の科学的記述に偶然が入り込み、カオス理論のおかげで、この不確実性の一部が理解できるようになりました。したがって、動的システムの定性的特性を解釈できるため、正確に計算しなくてもその動作のアイデアが得られます。すべては原因と結果のランダムな順序によって説明され、それぞれの出来事は因果関係の原則によって決定されます。宇宙全体は決定的ですが、必ず「混沌」が生じます。