最終更新日: 2025 年 10 月 6 日

安定性とカオス: 太陽系における軌道調和の限界

驚くほど精密な天体力学

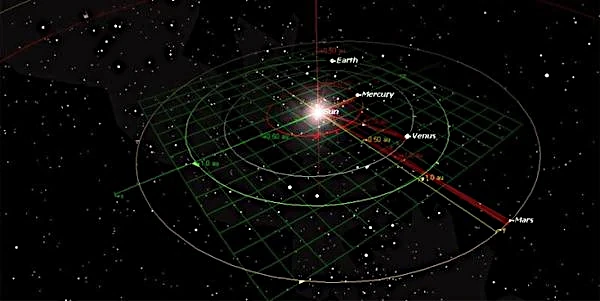
ザ惑星軌道太陽系の速度は、重力と各惑星の接線速度のバランスの結果です。が定式化した万有引力の法則によると、アイザック・ニュートン(1643-1727) では、2 つの質量体 \(m_1\) と \(m_2\) が力で互いに引き付けられます。 \[ F = G \frac{m_1 m_2}{r^2} \] ここで、 \(G = 6{,}674 \times 10^{-11}\ \text{N·m}^2·\text{kg}^{-2}\) は重力定数です。この相互作用により、次の法則に従って軌道が生成されます。ヨハネス・ケプラー(1571-1630) は楕円形で、太陽が焦点の 1 つを占めています。

ケプラーからラプラスへ: 安定性の追求

太陽系の安定性は長い間議論の対象となってきました。ピエール＝シモン・ラプラス(1749-1827) の一環として、デモンストレーションを行いました。撹乱理論、惑星間の共鳴は長期間にわたって互いに補償し、それによって長期的な安定性が確保される可能性があると考えられています。ただし、木星と土星の間で観察されるような軌道共鳴効果 (5:2 共鳴) は、経年変化。

決定論からカオスへ

20世紀におけるカオス理論の導入、特にアンリ・ポアンカレ(1854-1912)、天体力学の古典的なビジョンを覆しました。彼は、完全に決定論的な法則に従うシステムであっても、長期的には予測できない動作を示す可能性があることを示しました。太陽系の場合、運動方程式は非線形になり、初期条件の影響を受けやすくなります。複数の重力相互作用により、位相シフトや不安定性が生じる可能性があります。したがって、太陽系は数百万年にわたって安定しているように見えますが、最新の数値シミュレーションでは、特定の軌道が数億年後に発散する可能性があることが示されています。

共鳴: 軌道調和の柱

軌道共鳴とスピン軌道共鳴は、惑星バレエの一貫性を部分的に保証します。たとえば、水星と太陽の間の 3:2 の共鳴はその回転を安定させますが、イオ、エウロパ、ガニメデ (木星の衛星) の間の 1:2:4 の共鳴は多体系の動的バランスを示しています。

公転周期間のこれらの整数比により、重力擾乱を規則的に再分配することができ、短期的な混乱が制限されます。

太陽系の主な共鳴
関係機関	共鳴の種類	軌道比	ダイナミックエフェクト
水星 – 太陽	スピン軌道	3:2	潮汐トルクを最小限に抑えることで水星の自転を安定させます。完全なロックと自由回転の間のバランスをとり、半球間の極端な温度勾配を軽減します。
月 – 地球	スピン軌道	1:1	同期回転: 月は常に同じ顔を示します。潮汐の消失が進行し、地球の自転が遅くなり、月からの軌道距離が遅くなります (~3.8 cm/年)。
イオ – ヨーロッパ – ガニメデ	多重軌道	1:2:4	イオの軌道離心率を維持し、激しい潮汐加熱（火山活動）を引き起こします。内部の木星系を安定させ、二次ラプラス共鳴を調節します。
海王星 – 冥王星	オービタル	3:2	接近遭遇を防ぐ: 海王星の位相が 90° ずれている場合、冥王星は常に近日点を通過します。軌道が幾何学的に交差しているにもかかわらず、長期的な安定化が見られます。
木星 – 土星	永劫軌道	5:2	惑星の離心率の遅い変調（長周期共鳴）を引き起こします。太陽系全体の安定性と永年ラスカー周期 (約 100,000 年) に影響を与えます。
エンケラドゥス – ディオネ	オービタル	2:1	エンケラドゥスの離心率の周期的なポンピングを引き起こし、散逸する潮汐力を維持します。氷河下の海と南極で観察される極氷火山活動に栄養を与えています。
ミマス – テティス	オービタル	2:1	軌道傾斜角を安定させ、土星の環の分割に重力の影響を与えます。共鳴構造（密度波と空孔）の作成。
小惑星 – 木星 (カークウッドギャップ)	オービタル	3:1、5:2、2:1	木星との強い共鳴により小惑星の離心率が増大し、小惑星がメインベルトから弾き出される原因となります。空のゾーン (カークウッドギャップ) とカオスな軌道の形成。
ν6共鳴（土星）	世俗的な	変数	小惑星の近日点歳差運動と土星の近日点運動の同期。火星または地球と交差するまで離心率は徐々に増加し、太陽系の内部への放出と潜在的な流星体の生成につながります。
ν5共鳴（木星）	世俗的な	変数	小天体の近日点歳差運動と木星の近日点運動とのカップリング。離心率と傾斜角のサイクルを修正し、惑星の永年力学を構造化し、海王星横断共鳴に影響を与えます。

注意:
流星体: 大気との相互作用の前に、惑星間空間を移動する小さな固体。
隕石: 天体 (地球、月、火星など) の表面に到達した流星の固体の残骸。
流星：流星が大気圏に突入する際に（摩擦や電離によって）生じる発光現象。

外惑星軌道

内側の軌道 (水星、金星、地球、火星) は高速かつコンパクトで人口密度が高いのに対し、外側の軌道 (木星、土星、天王星、海王星) は大きくて巨大で、強い重力共鳴によって支配されており、太陽系の階層と調和を示しています。

ダイナミックかつ繊細なバランス

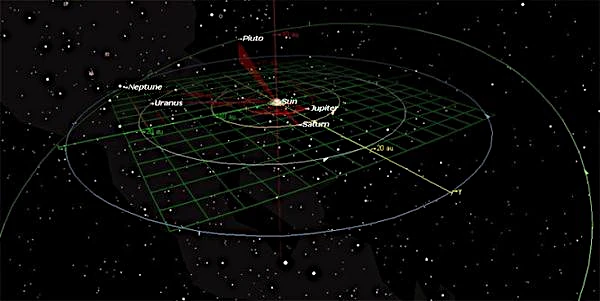
見かけの規則性にもかかわらず、惑星の軌道は、相互の擾乱、潮汐力、エネルギー散逸の複合効果の下でゆっくりと進化します。太陽系の調和は、秩序と混沌の間のこのダイナミックなバランスにあります。

軌道調和は固定されていません。潮汐力、太陽の質量損失、および軽微な重力相互作用により、軌道パラメータはゆっくりと変化します。離心率 \(e\) 、傾き \(i\) 、近日点経度 \(\omega\) は数万年の周期で変化します。これらの変動は、次のサイクルで表されます。ミルティン・ミランコビッチ（1879-1958）、地球の気候に直接影響を与えます。

太陽系の惑星の平均軌道パラメータ
惑星	長半径 (UA)	偏心	傾き(°)	公転周期（年）
水銀	0.387	0.2056	7.00	0.24
金星	0.723	0.0068	3.39	0.62
地球	1,000	0.0167	0.00	1.00
行進	1,524	0.0934	1.85	1.88
木星	5,203	0.0484	1.31	11.86
土星	9,537	0.0542	2.49	29.46
天王星	19,191	0.0472	0.77	84.01
ネプチューン	30,068	0.0086	1.77	164.8

ソース：NASA – ジェット推進研究所 (太陽系力学)そしてLaskar, J. (1999) – 太陽系の安定性の限界。

45億年にわたる太陽系のダイナミックな進化と安定性

1. 原初のカオスと惑星の放出

その間、太陽系の形成、この系には惑星、惑星胚、微惑星がはるかに多く存在していました。この初期期間は、しばしば次のように呼ばれます。混沌とした、頻繁な衝突、激しいエネルギー交換、複数の重力擾乱が特徴でした。数値シミュレーションによると、特定の惑星または惑星の胚は、星間空間に向かって放出されるまたは、より巨大な物体に吸収されます。このプロセスのダイナミックなリラクゼーションこれにより、重力階層と互換性のある軌道だけを残し、共鳴を安定化させて系を浄化することが可能になりました。

したがって、原始的なカオスは、軌道の自然選択惑星体。これらの出来事の痕跡は、今日でも小惑星帯、彗星集団、海王星横断天体で観察できます。

2. 質量の階層と準積分可能性

この初期段階の後、太陽系約 45 億年にわたり、重力共鳴、エネルギー散逸、質量階層間の微妙なバランスから生じたものです。相互作用の複雑さにもかかわらず、システムは全体的には変わりませんほぼ統合可能ハミルトン力学の意味では、小さな混乱は全体的な混乱を引き起こしませんでした。

最初の理由は次のとおりです。質量の階層的分布。ザ太陽と惑星の比率(\(M_{\odot}/M_{J} \およそ 10^3\)) は重心に準定常性を与えます。惑星のダイナミクスは一連のものとして扱うことができます。世俗的な運動の解によると、平均軌道の周りでピエール＝シモン・ラプラス(1749–1827) およびジョゼフ＝ルイ・ラグランジュ（1736–1813）。

3. 共振の安定化

ザ共鳴を安定させる規制的な役割を果たします。ほぼ整数の周期比 (例: 5:2)木星そして土星) 偏心や傾斜が無限に拡大するのを防ぎます。これらの共鳴は、重力ポテンシャル井戸と同様に、振動を制限された位相ゾーンに限定することにより、軌道エネルギーの伝達を制限します。

4. 限られたカオスと現在のダイナミクス

最近のデジタル作品 (ジャック・ラスカー、1989–2010) は、太陽系の内部が限定的な決定論的カオス: 軌道要素は長期的には予測不可能に変化しますが、総エネルギーと最初の積分により巨視的な発散は防止されます。言い換えれば、カオスは局所的に存在しますが、コンテンツ重力系のグローバルトポロジーによる。

したがって、数十億年にわたる安定は、混乱がないことによって生じるのではなく、混乱によって生じるのです。規則性と限定された不安定性の共存。共鳴と質量の階層によって維持されているこの脆弱なバランスは、最初の混沌段階の終わり以来主要な惑星が放出されていない理由を説明しています。