Estabilidade e Caos: Os Limites da Harmonia Orbital do Sistema Solar

Uma mecânica celeste de precisão fascinante

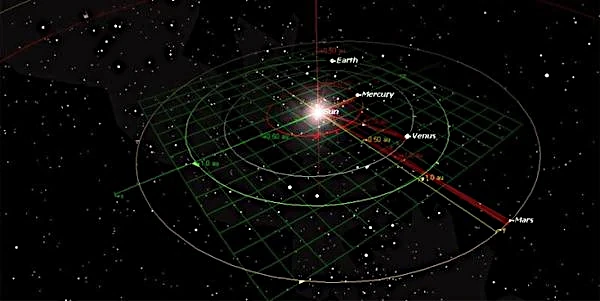
As órbitas planetárias (movimentos periódicos dos planetas em torno do Sol) do Sistema Solar são o resultado de um equilíbrio entre a gravidade e a velocidade tangencial de cada planeta. Segundo a lei da gravitação universal formulada por Isaac Newton (1643-1727), dois corpos de massas \(m_1\) e \(m_2\) atraem-se com uma força: \[ F = G \frac{m_1 m_2}{r^2} \] onde \(G = 6.674 \times 10^{-11}\ \text{N·m}^2·\text{kg}^{-2}\) é a constante gravitacional. Esta interação gera trajetórias que, segundo as leis de Johannes Kepler (1571-1630), são elípticas, com o Sol a ocupar um dos focos.

De Kepler a Laplace: a busca pela estabilidade

A estabilidade do Sistema Solar tem sido durante muito tempo um tema de controvérsia. Pierre-Simon Laplace (1749-1827) demonstrou, no quadro da teoria das perturbações (aproximação matemática utilizada para tratar pequenas perturbações), que as ressonâncias entre planetas podiam compensar-se durante longos períodos, assegurando assim uma estabilidade secular. No entanto, os efeitos de ressonância orbital, como os observados entre Júpiter e Saturno (ressonância 5:2), introduzem variações lentas chamadas variações seculares (mudanças progressivas e periódicas dos parâmetros orbitais).

Do determinismo ao caos

A introdução da teoria do caos no século XX, particularmente por Henri Poincaré (1854-1912), revolucionou a visão clássica da mecânica celeste. Mostrou que mesmo um sistema obedecendo a leis perfeitamente deterministas pode apresentar comportamentos imprevisíveis a longo prazo. No caso do Sistema Solar, as equações do movimento tornam-se não lineares e sensíveis às condições iniciais. As múltiplas interações gravitacionais podem levar a defasagens e até a instabilidades. Assim, embora o Sistema Solar pareça estável durante milhões de anos, as simulações numéricas modernas mostram que algumas órbitas poderão divergir após algumas centenas de milhões de anos.

As ressonâncias: pilares da harmonia orbital

As ressonâncias orbital e de rotação-órbita asseguram parcialmente a coerência do ballet planetário. Por exemplo, a ressonância 3:2 entre Mercúrio e o Sol estabiliza a sua rotação, enquanto a ressonância 1:2:4 entre Io, Europa e Ganimedes (luas de Júpiter) ilustra o equilíbrio dinâmico de um sistema de vários corpos.

Estas relações inteiras entre períodos orbitais permitem a redistribuição regular das perturbações gravitacionais, limitando assim o caos a curto prazo.

N.B.:
Meteoroide: pequeno corpo sólido que se move no espaço interplanetário, antes de qualquer interação com uma atmosfera.
Meteorito: resíduo sólido de um meteoroide que atinge a superfície de um corpo celeste (Terra, Lua, Marte…).
Meteoro: fenómeno luminoso produzido quando um meteoroide entra numa atmosfera (por fricção e ionização).

Órbitas planetárias exteriores

As órbitas internas (Mercúrio, Vénus, Terra, Marte) são rápidas, compactas e densamente povoadas, enquanto as órbitas exteriores (Júpiter, Saturno, Urano, Neptuno) são amplas, massivas e governadas por fortes ressonâncias gravitacionais, ilustrando a hierarquia e a harmonia do Sistema Solar.

Um equilíbrio dinâmico e frágil

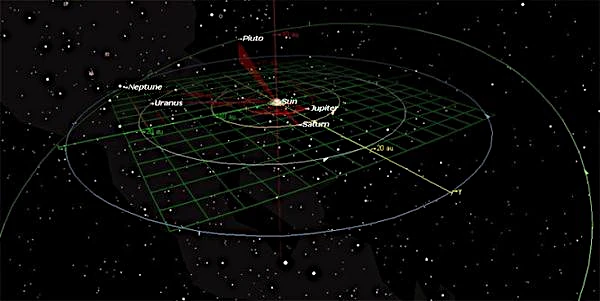
Apesar da sua aparente regularidade, as órbitas planetárias evoluem lentamente sob o efeito combinado das perturbações mútuas, das forças de maré e da dissipação de energia. A harmonia do Sistema Solar reside neste equilíbrio dinâmico entre ordem e caos.

A harmonia orbital não é fixa. As forças de maré, a perda de massa solar e as interações gravitacionais menores modificam lentamente os parâmetros orbitais. A excentricidade \(e\), a inclinação \(i\) e a longitude do periélio \(\omega\) variam segundo ciclos de várias dezenas de milhares de anos. Estas variações, descritas pelos ciclos de Milutin Milankovitch (1879-1958), influenciam diretamente o clima terrestre.

Evolução dinâmica e estabilidade do Sistema Solar ao longo de 4,5 mil milhões de anos

Caos primordial e ejeção de planetas

Durante a formação do Sistema Solar, o sistema estava muito mais povoado em planetas, embriões planetários e planetesimais. Este período inicial, frequentemente qualificado de caótico (fase em que os corpos interagem fortemente e de forma caótica), foi caracterizado por colisões frequentes, intensas trocas energéticas e múltiplas perturbações gravitacionais. As simulações numéricas indicam que alguns planetas ou embriões planetários foram ejetados para o espaço interestelar ou absorvidos por corpos mais massivos. Este processo de relaxação dinâmica (eliminação de trajetórias instáveis por interações gravitacionais) permitiu depurar o sistema, deixando apenas órbitas compatíveis com a hierarquia gravitacional e as ressonâncias estabilizadoras.

O caos primordial foi, portanto, essencial para a seleção natural orbital dos corpos planetários. Os vestígios destes eventos ainda são observáveis hoje no cinturão de asteroides, nas populações de cometas e nos objetos transneptunianos.

Hierarquia de massas e quasi-integrabilidade

Após esta fase inicial, a notável estabilidade do Sistema Solar durante aproximadamente 4,5 mil milhões de anos resulta de um equilíbrio subtil entre ressonâncias gravitacionais, dissipação de energia e hierarquia de massas. Apesar da complexidade das suas interações, o sistema permanece globalmente quasi-integrável no sentido da mecânica hamiltoniana: as pequenas perturbações não conduziram a um caos generalizado.

A primeira razão reside na distribuição hierárquica das massas. A relação Sol/planetas (relação de massa entre o Sol e os planetas) (\(M_{\odot}/M_{J} \approx 10^3\)) confere ao centro de massa uma quase-estacionariedade. A dinâmica planetária pode então ser tratada como uma série de movimentos seculares (movimentos descritos por uma expansão em pequenas perturbações) em torno de órbitas médias, segundo as soluções de Pierre-Simon Laplace (1749–1827) e Joseph-Louis Lagrange (1736–1813).

Ressonâncias estabilizadoras

As ressonâncias estabilizadoras desempenham um papel regulador. As relações de períodos quase inteiras (por exemplo 5:2 para Júpiter e Saturno) impedem uma amplificação indefinida das excentricidades e inclinações. Estas ressonâncias limitam a transferência de energia orbital confinando as oscilações em zonas de fase restritas, análogas a poços de potencial gravitacional.

Caos limitado e dinâmica atual

Os trabalhos numéricos recentes (Jacques Laskar, 1989–2010) mostraram que o Sistema Solar interno apresenta um caos determinista limitado (comportamento caótico mas limitado por restrições de conservação): os elementos orbitais variam de forma imprevisível a longo prazo, mas a energia total e as integrais primeiras impedem qualquer divergência macroscópica. Por outras palavras, o caos existe localmente, mas está contido pela topologia global do sistema gravitacional.

Assim, a estabilidade durante milhares de milhões de anos não resulta de uma ausência de caos, mas de uma coexistência entre regularidade e instabilidade confinada. Este frágil equilíbrio, mantido pelas ressonâncias e pela hierarquia de massas, explica porque nenhum planeta maior foi ejetado desde o fim da fase caótica inicial.

Perspetivas futuras e destino a longo prazo do Sistema Solar

A evolução do Sol e o fim dos planetas internos

Embora o Sistema Solar tenha demonstrado uma estabilidade notável durante 4,5 mil milhões de anos, o seu destino a longo prazo está inexoravelmente ligado à evolução do Sol. Daqui a aproximadamente 5 mil milhões de anos, o Sol entrará na sua fase de gigante vermelha, aumentando consideravelmente a sua luminosidade e raio. Esta expansão provocará a vaporização dos planetas internos (Mercúrio, Vénus e provavelmente a Terra) e a modificação profunda das órbitas dos planetas externos. As simulações numéricas (Schröder & Smith, 2008) sugerem que o Sistema Solar tal como o conhecemos deixará de existir muito antes de as instabilidades caóticas internas o desestabilizarem.

Variações orbitais e impactos climáticos futuros

A uma escala mais curta (algumas centenas de milhões de anos), as variações dos parâmetros orbitais da Terra continuarão a influenciar o seu clima. Os ciclos de Milankovitch deverão persistir, mas a sua amplitude poderá ser modulada pelas interações gravitacionais com os planetas externos. Os trabalhos de Laskar et al. (2011) indicam que a excentricidade terrestre poderá atingir valores extremos (até 0.06) nos próximos 200 milhões de anos, afetando significativamente os ciclos glaciares.

Evolução dos objetos transneptunianos e da nuvem de Oort

Finalmente, os objetos transneptunianos, particularmente Plutão e outros planetas anões, continuarão a evoluir sob a influência das ressonâncias com Neptuno. O cinturão de Kuiper e a nuvem de Oort sofrerão perturbações gravitacionais lentas, potencialmente responsáveis por futuras chuvas de cometas em escalas de tempo de várias centenas de milhões de anos.