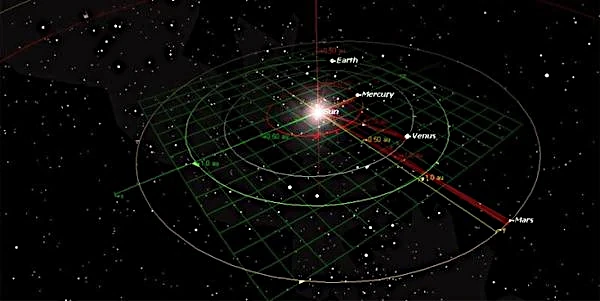
Les orbites planétaires du Système solaire sont le résultat d’un équilibre entre la gravité et la vitesse tangentielle de chaque planète. Selon la loi de la gravitation universelle formulée par Isaac Newton (1643-1727), deux corps de masses \(m_1\) et \(m_2\) s’attirent avec une force : \[ F = G \frac{m_1 m_2}{r^2} \] où \(G = 6{,}674 \times 10^{-11}\ \text{N·m}^2·\text{kg}^{-2}\) est la constante gravitationnelle. Cette interaction engendre des trajectoires qui, selon les lois de Johannes Kepler (1571-1630), sont elliptiques, avec le Soleil occupant l’un des foyers.
La stabilité du Système solaire a longtemps été un sujet de controverse. Pierre-Simon Laplace (1749-1827) démontra, dans le cadre de la théorie des perturbations, que les résonances entre planètes pouvaient se compenser sur de longues durées, assurant ainsi une stabilité séculaire. Cependant, des effets de résonance orbitale, comme ceux observés entre Jupiter et Saturne (résonance 5:2), introduisent des variations lentes appelées variations séculaires.
L’introduction de la théorie du chaos au XXᵉ siècle, notamment par Henri Poincaré (1854-1912), a bouleversé la vision classique de la mécanique céleste. Il a montré que même un système obéissant à des lois parfaitement déterministes pouvait présenter des comportements imprévisibles sur le long terme. Dans le cas du Système solaire, les équations du mouvement deviennent non linéaires et sensibles aux conditions initiales. Les interactions gravitationnelles multiples peuvent mener à des déphasages, voire à des instabilités. Ainsi, bien que le Système solaire semble stable sur des millions d’années, les simulations numériques modernes montrent que certaines orbites pourraient diverger après quelques centaines de millions d’années.
Les résonances orbitale et spin-orbitale assurent partiellement la cohérence du ballet planétaire. Par exemple, la résonance 3:2 entre Mercure et le Soleil stabilise sa rotation, tandis que la résonance 1:2:4 entre Io, Europe et Ganymède (lunes de Jupiter) illustre l’équilibre dynamique d’un système à plusieurs corps.
Ces rapports entiers entre périodes orbitales permettent la redistribution régulière des perturbations gravitationnelles, limitant ainsi le chaos à court terme.
| Corps concernés | Type de résonance | Rapport orbital | Effet dynamique |
|---|---|---|---|
| Mercure – Soleil | Spin–orbitale | 3:2 | Stabilise la rotation de Mercure en minimisant les couples de marée ; équilibre entre verrouillage complet et rotation libre, réduisant les gradients thermiques extrêmes entre hémisphères. |
| Lune – Terre | Spin–orbitale | 1:1 | Rotation synchrone : la Lune présente toujours la même face ; dissipation maréale progressive, ralentissement de la rotation terrestre et éloignement orbital de la Lune (~3,8 cm/an). |
| Io – Europe – Ganymède | Orbitale multiple | 1:2:4 | Maintient l’excentricité orbitale d’Io, induisant un chauffage de marée intense (activité volcanique) ; stabilise le système jovien interne et régule les résonances secondaires de Laplace. |
| Neptune – Pluton | Orbitale | 3:2 | Empêche les rencontres proches : Pluton passe toujours au périhélie lorsque Neptune est à 90° de déphasage ; stabilisation à long terme malgré le croisement géométrique des orbites. |
| Jupiter – Saturne | Orbitale séculaire | 5:2 | Provoque une modulation lente des excentricités planétaires (résonance de grande période) ; influence la stabilité globale du Système solaire et les cycles séculaires de Laskar (~100 000 ans). |
| Encelade – Dioné | Orbitale | 2:1 | Induit un pompage périodique de l’excentricité d’Encelade, entretenant des forces de marée dissipatives ; alimente son océan sous-glaciaire et l’activité cryovolcanique observée au pôle sud. |
| Mimas – Téthys | Orbitale | 2:1 | Stabilise les inclinaisons orbitales et influence gravitationnellement les divisions dans les anneaux de Saturne ; création de structures résonantes (ondes de densité et lacunes). |
| Astéroïdes – Jupiter (lacunes de Kirkwood) | Orbitale | 3:1, 5:2, 2:1 | Les résonances fortes avec Jupiter augmentent l’excentricité des astéroïdes, provoquant leur éjection de la ceinture principale ; formation de zones vides (lacunes de Kirkwood) et de trajectoires chaotiques. |
| Résonance ν6 (Saturne) | Séculaire | Variable | Synchronisation entre la précession du périhélie des astéroïdes et celle de Saturne ; augmentation progressive de l’excentricité jusqu’à l’intersection avec Mars ou la Terre, entraînant l’éjection vers l’intérieur du Système solaire et la production de météoroïdes potentiels. |
| Résonance ν5 (Jupiter) | Séculaire | Variable | Couplage entre la précession du périhélie des petits corps et celle de Jupiter ; modifie les cycles d’excentricité et d’inclinaison, structure la dynamique séculaire des planètes et influence les résonances transneptuniennes. |
N.B.:
Météoroïde :petit corps solide se déplaçant dans l’espace interplanétaire, avant toute interaction avec une atmosphère.
Météoroïte : résidu solide d’un météoroïde qui atteint la surface d’un astre (Terre, Lune, Mars…).
Météore : phénomène lumineux produit lorsqu’un météoroïde entre dans une atmosphère (par frottement et ionisation).
Les orbites intérieures (Mercure, Vénus, Terre, Mars) sont rapides, compactes et densément peuplées, tandis que les orbites extérieures (Jupiter, Saturne, Uranus, Neptune) sont larges, massives et gouvernées par de fortes résonances gravitationnelles, illustrant la hiérarchie et l’harmonie du Système solaire.
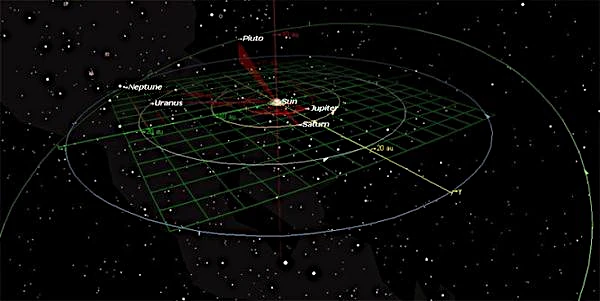
Malgré leur apparente régularité, les orbites planétaires évoluent lentement sous l’effet combiné des perturbations mutuelles, des forces de marée et de la dissipation énergétique. L’harmonie du Système solaire réside dans cet équilibre dynamique entre ordre et chaos.
L’harmonie orbitale n’est pas figée. Les forces de marée, la perte de masse solaire et les interactions gravitationnelles mineures modifient lentement les paramètres orbitaux. L’excentricité \(e\), l’inclinaison \(i\) et la longitude du périhélie \(\omega\) varient selon des cycles de plusieurs dizaines de milliers d’années. Ces variations, décrites par les cycles de Milutin Milankovitch (1879-1958), influencent directement le climat terrestre.
| Planète | Demi-grand axe (UA) | Excentricité | Inclinaison (°) | Période orbitale (années) |
|---|---|---|---|---|
| Mercure | 0,387 | 0,2056 | 7,00 | 0,24 |
| Vénus | 0,723 | 0,0068 | 3,39 | 0,62 |
| Terre | 1,000 | 0,0167 | 0,00 | 1,00 |
| Mars | 1,524 | 0,0934 | 1,85 | 1,88 |
| Jupiter | 5,203 | 0,0484 | 1,31 | 11,86 |
| Saturne | 9,537 | 0,0542 | 2,49 | 29,46 |
| Uranus | 19,191 | 0,0472 | 0,77 | 84,01 |
| Neptune | 30,068 | 0,0086 | 1,77 | 164,8 |
Source : NASA – Jet Propulsion Laboratory (Solar System Dynamics) et Laskar, J. (1999) – The Limits of Stability in the Solar System.
Lors de la formation du Système solaire, le système était beaucoup plus peuplé en planètes, embryons planétaires et planétésimaux. Cette période initiale, souvent qualifiée de chaotique, a été caractérisée par des collisions fréquentes, des échanges énergétiques intenses et des perturbations gravitationnelles multiples. Les simulations numériques indiquent que certaines planètes ou embryons planétaires ont été éjectés vers l’espace interstellaire ou absorbés par des corps plus massifs. Ce processus de relaxation dynamique a permis d’épurer le système, ne laissant que des orbites compatibles avec la hiérarchie gravitationnelle et les résonances stabilisatrices.
Le chaos primordial a donc été essentiel pour la sélection naturelle orbitale des corps planétaires. Les traces de ces événements sont encore observables aujourd’hui dans la ceinture d’astéroïdes, les populations de comètes et les objets transneptuniens.
Après cette phase initiale, la stabilité remarquable du Système solaire depuis environ 4,5 milliards d’années résulte d’un équilibre subtil entre résonances gravitationnelles, dissipation d’énergie et hiérarchie des masses. Malgré la complexité de ses interactions, le système demeure globalement quasi intégrable au sens de la mécanique hamiltonienne : les petites perturbations n’ont pas conduit à un chaos généralisé.
La première raison tient à la distribution hiérarchique des masses. Le rapport Soleil/planètes (\(M_{\odot}/M_{J} \approx 10^3\)) confère au centre de masse une quasi-stationarité. La dynamique planétaire peut alors être traitée comme une série de mouvements séculaires autour d’orbites moyennes, selon les solutions de Pierre-Simon Laplace (1749–1827) et Joseph-Louis Lagrange (1736–1813).
Les résonances stabilisatrices jouent un rôle régulateur. Les rapports de périodes quasi entiers (par exemple 5:2 pour Jupiter et Saturne) empêchent une amplification indéfinie des excentricités et inclinaisons. Ces résonances limitent le transfert d’énergie orbitale en confinant les oscillations dans des zones de phase restreintes, analogues à des puits de potentiel gravitationnel.
Les travaux numériques récents (Jacques Laskar, 1989–2010) ont montré que le Système solaire interne présente un chaos déterministe limité : les éléments orbitaux varient de manière imprévisible à long terme, mais l’énergie totale et les intégrales premières empêchent toute divergence macroscopique. Autrement dit, le chaos existe localement, mais il est contenu par la topologie globale du système gravitationnel.
Ainsi, la stabilité sur des milliards d’années ne résulte pas d’une absence de chaos, mais d’une coexistence entre régularité et instabilité confinée. Ce fragile équilibre, maintenu par les résonances et la hiérarchie des masses, explique pourquoi aucune planète majeure n’a été éjectée depuis la fin de la phase chaotique initiale.
Système solaire vs Systèmes Stellaires : Comparaison des Systèmes Planétaires 
Le Paradoxe du Jeune Soleil Faible : Pourquoi la Terre Primitive n’était pas Gelée ? 
380 milliards de milliards de mégawatts : La Débauche d’Énergie Solaire 
L'écliptique ou l'orbite apparente du Soleil 
Maximum et minimum solaire 
Comment
peser le soleil ? 
Soleil : Quand l’astre jaune devient bleu 
Explication du 8 de l'analemme 
Simulateur, la révolution des planètes autour du Soleil 
Ligne des Glaces : la Limite qui a Façonné les Planètes 
Voyage touristique dans le système solaire 
Les Taches Solaires et le Cycle Solaire : Du Minimum au Maximum 
Le voyage infernal du photon ou marche aléatoire 
Dynamique des Cycles Solaires et Mécanismes Physiques des Éruptions Solaires 
Les grains de Baily dans une éclipse solaire 
Naissance, Vie et Mort du Soleil : Chronique d’une Étoile Moyenne 
Grains de Baily ou perles de lumière 
Lumières du Soleil et longueurs d'onde 
La formation chaotique du système solaire 
Tempêtes Solaires et Scénario Catastrophe 
Protubérances Solaires : Des Filaments de Matière dans l'Atmosphère Solaire 
Pourquoi le Soleil tourne si lentement ? Le mystère du moment cinétique manquant 
Transit de Vénus du 5 et 6 juin 2012 : Dernière Traversée Avant un Siècle 
Transit de la Lune devant le Soleil vu depuis l'espace en 2007 
Vents solaires : un phénomène clé de l’espace interplanétaire 
Héliosphère : Aux Frontières du Système Solaire
Chaos et sensibilité aux conditions initiales 
Stabilité et Chaos : Les Limites de l’Harmonie Orbitale du Système Solaire