Letzte Aktualisierung: 6. Oktober 2025

Stabilität und Chaos: Die Grenzen der Orbitalharmonie im Sonnensystem

Faszinierend präzise Himmelsmechanik

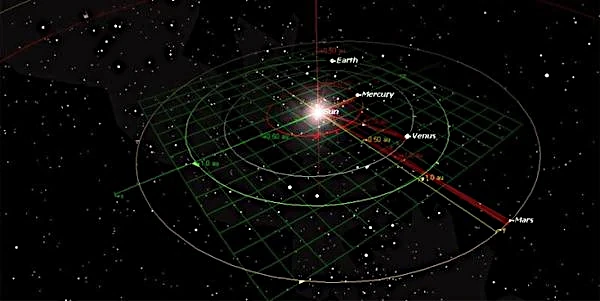
DERPlanetenbahnendes Sonnensystems sind das Ergebnis eines Gleichgewichts zwischen der Schwerkraft und der Tangentialgeschwindigkeit jedes Planeten. Nach dem Gesetz der universellen Gravitation formuliert vonIsaac Newton(1643-1727) ziehen sich zwei Körper mit den Massen \(m_1\) und \(m_2\) gegenseitig mit einer Kraft an: \[ F = G \frac{m_1 m_2}{r^2} \] wobei \(G = 6{,}674 \times 10^{-11}\ \text{N·m}^2·\text{kg}^{-2}\) die Gravitationskonstante ist. Diese Interaktion erzeugt Flugbahnen, die nach den Gesetzen vonJohannes Kepler(1571-1630) sind elliptisch, wobei die Sonne einen der Brennpunkte einnimmt.

Von Kepler bis Laplace: das Streben nach Stabilität

Die Stabilität des Sonnensystems ist seit langem Gegenstand von Kontroversen.Pierre-Simon Laplace(1749-1827) demonstrierte im Rahmen derStörungstheorie, dass Resonanzen zwischen Planeten sich über lange Zeiträume gegenseitig kompensieren und so säkulare Stabilität gewährleisten könnten. Allerdings führen Orbitalresonanzeffekte, wie sie zwischen Jupiter und Saturn beobachtet werden (5:2-Resonanz), zu langsamen Schwankungen, die als „langsam“ bezeichnet werdenweltliche Variationen.

Vom Determinismus zum Chaos

Die Einführung der Chaostheorie im 20. Jahrhundert, insbesondere durchHenri Poincaré(1854-1912) stellte die klassische Vision der Himmelsmechanik auf den Kopf. Er zeigte, dass selbst ein System, das vollkommen deterministischen Gesetzen gehorcht, langfristig unvorhersehbares Verhalten zeigen kann. Im Fall des Sonnensystems werden die Bewegungsgleichungen nichtlinear und empfindlich gegenüber den Anfangsbedingungen. Mehrere Gravitationswechselwirkungen können zu Phasenverschiebungen oder sogar Instabilitäten führen. Obwohl das Sonnensystem über Millionen von Jahren stabil zu sein scheint, zeigen moderne numerische Simulationen, dass bestimmte Umlaufbahnen nach einigen hundert Millionen Jahren auseinanderlaufen könnten.

Resonanzen: Säulen der Orbitalharmonie

Die Orbital- und Spin-Orbital-Resonanzen sorgen teilweise für die Kohärenz des Planetenballetts. Beispielsweise stabilisiert die 3:2-Resonanz zwischen Merkur und der Sonne ihre Rotation, während die 1:2:4-Resonanz zwischen Io, Europa und Ganymed (Jupitermonden) das dynamische Gleichgewicht eines Vielkörpersystems veranschaulicht.

Diese ganzzahligen Verhältnisse zwischen Umlaufperioden ermöglichen die regelmäßige Umverteilung von Gravitationsstörungen und begrenzen so kurzfristiges Chaos.

Hauptresonanzen des Sonnensystems
Betroffene Stellen	Art der Resonanz	Orbitalverhältnis	Dynamischer Effekt
Merkur – Sonne	Spin-Orbital	3:2	Stabilisiert die Rotation von Merkur durch Minimierung der Gezeitendrehmomente; Gleichgewicht zwischen vollständiger Verriegelung und freier Rotation, wodurch extreme Wärmegradienten zwischen den Hemisphären reduziert werden.
Mond – Erde	Spin-Orbital	1:1	Synchrone Rotation: Der Mond zeigt immer das gleiche Gesicht; fortschreitende Gezeitendissipation, Verlangsamung der Erdrotation und Umlaufentfernung vom Mond (~3,8 cm/Jahr).
Io – Europa – Ganymed	Mehrere Orbitale	1:2:4	Behält die Exzentrizität der Umlaufbahn von Io bei und führt zu einer starken Gezeitenerwärmung (vulkanische Aktivität); stabilisiert das innere Jupitersystem und reguliert sekundäre Laplace-Resonanzen.
Neptun – Pluto	Orbital	3:2	Verhindert enge Begegnungen: Pluto passiert immer dann sein Perihel, wenn Neptun um 90° phasenverschoben ist; langfristige Stabilisierung trotz der geometrischen Kreuzung der Umlaufbahnen.
Jupiter – Saturn	Weltliches Orbital	5:2	Verursacht eine langsame Modulation der Planetenexzentrizitäten (Resonanz mit langer Periode); beeinflusst die Gesamtstabilität des Sonnensystems und die säkularen Laskar-Zyklen (~100.000 Jahre).
Enceladus – Dione	Orbital	2:1	Induziert ein periodisches Pumpen der Exzentrizität von Enceladus und hält dissipative Gezeitenkräfte aufrecht; speist seinen subglazialen Ozean und die am Südpol beobachtete kryovulkanische Aktivität.
Mimas – Tethys	Orbital	2:1	Stabilisiert die Orbitalneigungen und beeinflusst durch die Schwerkraft die Teilungen in den Saturnringen; Entstehung resonanter Strukturen (Dichtewellen und Leerstellen).
Asteroiden – Jupiter (Kirkwood-Lücken)	Orbital	3:1, 5:2, 2:1	Starke Resonanzen mit Jupiter erhöhen die Exzentrizität von Asteroiden und führen dazu, dass sie aus dem Hauptgürtel herausgeschleudert werden. Bildung leerer Zonen (Kirkwood-Lücken) und chaotischer Flugbahnen.
ν6 Resonanz (Saturn)	Weltlich	Variable	Synchronisation zwischen der Perihelpräzession von Asteroiden und der des Saturn; progressive Zunahme der Exzentrizität bis zum Schnittpunkt mit Mars oder Erde, was zum Auswurf in das Innere des Sonnensystems und zur Produktion potenzieller Meteoroiden führt.
ν5-Resonanz (Jupiter)	Weltlich	Variable	Kopplung zwischen der Perihelpräzession kleiner Körper und der des Jupiter; modifiziert Exzentrizitäts- und Inklinationszyklen, strukturiert die säkulare Dynamik der Planeten und beeinflusst transneptunische Resonanzen.

Hinweis:
Meteoroid: kleiner fester Körper, der sich im interplanetaren Raum bewegt, bevor er mit der Atmosphäre interagiert.
Meteorit: fester Rückstand eines Meteoroiden, der die Oberfläche eines Himmelskörpers (Erde, Mond, Mars usw.) erreicht.
Meteor: Lichtphänomen, das entsteht, wenn ein Meteoroid in die Atmosphäre eindringt (durch Reibung und Ionisation).

Äußere Planetenbahnen

Die inneren Umlaufbahnen (Merkur, Venus, Erde, Mars) sind schnell, kompakt und dicht besiedelt, während die äußeren Umlaufbahnen (Jupiter, Saturn, Uranus, Neptun) groß, massiv sind und von starken Gravitationsresonanzen bestimmt werden, was die Hierarchie und Harmonie des Sonnensystems veranschaulicht.

Ein dynamisches und fragiles Gleichgewicht

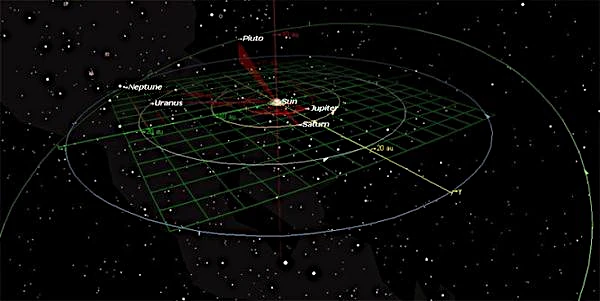
Trotz ihrer scheinbaren Regelmäßigkeit entwickeln sich Planetenbahnen langsam unter der kombinierten Wirkung gegenseitiger Störungen, Gezeitenkräfte und Energiedissipation. Die Harmonie des Sonnensystems liegt in diesem dynamischen Gleichgewicht zwischen Ordnung und Chaos.

Die Orbitalharmonie ist nicht festgelegt. Gezeitenkräfte, solarer Massenverlust und geringfügige Gravitationswechselwirkungen verändern langsam die Orbitalparameter. Die Exzentrizität \(e\), die Neigung \(i\) und die Länge des Perihels \(\omega\) variieren je nach Zyklen von mehreren Zehntausend Jahren. Diese Variationen, beschrieben durch die Zyklen vonMilutin Milankovitch(1879-1958) beeinflussen direkt das Klima der Erde.

Durchschnittliche Umlaufparameter der Planeten des Sonnensystems
Planet	Halbgroße Achse (UA)	Exzentrizität	Neigung (°)	Umlaufzeit (Jahre)
Quecksilber	0,387	0,2056	7.00	0,24
Venus	0,723	0,0068	3.39	0,62
Erde	1.000	0,0167	0,00	1,00
Marsch	1.524	0,0934	1,85	1,88
Jupiter	5.203	0,0484	1.31	11.86
Saturn	9.537	0,0542	2,49	29.46
Uranus	19.191	0,0472	0,77	84.01
Neptun	30.068	0,0086	1,77	164,8

Quelle :NASA – Jet Propulsion Laboratory (Dynamik des Sonnensystems)UndLaskar, J. (1999) – Die Grenzen der Stabilität im Sonnensystem.

Dynamische Entwicklung und Stabilität des Sonnensystems über 4,5 Milliarden Jahre

1. Urchaos und Planetenauswurf

Während derEntstehung des Sonnensystems, war das System viel stärker mit Planeten, Planetenembryonen und Planetesimalen bevölkert. Diese Anfangsphase wird oft als bezeichnetchaotischwar durch häufige Kollisionen, intensiven Energieaustausch und mehrere Gravitationsstörungen gekennzeichnet. Numerische Simulationen deuten darauf hin, dass es bestimmte Planeten oder Planetenembryonen gegeben hatin den interstellaren Raum geschleudertoder von massiveren Körpern absorbiert werden. Dieser Prozess vondynamische Entspannungermöglichte es, das System zu reinigen, sodass nur Umlaufbahnen übrig blieben, die mit der Gravitationshierarchie kompatibel waren und Resonanzen stabilisierten.

Das ursprüngliche Chaos war daher wesentlich für dieorbitale natürliche SelektionPlanetenkörper. Spuren dieser Ereignisse sind noch heute im Asteroidengürtel, in Kometenpopulationen und in transneptunischen Objekten zu beobachten.

2. Massenhierarchie und Quasiintegrabilität

Nach dieser Anfangsphase ist die bemerkenswerte Stabilität desSonnensystementsteht seit rund 4,5 Milliarden Jahren aus einem subtilen Gleichgewicht zwischen Gravitationsresonanzen, Energiedissipation und Massenhierarchie. Trotz der Komplexität seiner Wechselwirkungen bleibt das System ein Ganzesnahezu integrierbarim Sinne der Hamiltonschen Mechanik: Kleine Störungen führten nicht zu allgemeinem Chaos.

Der erste Grund liegt an derhierarchische Verteilung der Massen. DERVerhältnis Sonne/Planet(\(M_{\odot}/M_{J} \ approx 10^3\)) gibt dem Massenschwerpunkt Quasistationarität. Die Planetendynamik kann dann als eine Reihe von behandelt werdenweltliche Bewegungenum durchschnittliche Umlaufbahnen, gemäß den Lösungen vonPierre-Simon Laplace(1749–1827) undJoseph-Louis Lagrange (1736–1813).

3. Stabilisierung von Resonanzen

DERstabilisierende Resonanzeneine regulierende Rolle spielen. Nahezu ganzzahlige Periodenverhältnisse (z. B. 5:2 fürJupiterUndSaturn) verhindern eine unbegrenzte Verstärkung von Exzentrizitäten und Neigungen. Diese Resonanzen begrenzen die Übertragung von Orbitalenergie, indem sie die Schwingungen auf begrenzte Phasenzonen beschränken, analog zu Gravitationspotentialtöpfen.

4. Begrenztes Chaos und aktuelle Dynamik

Aktuelle digitale Werke (Jacques Laskar, 1989–2010) zeigte, dass das innere Sonnensystem eine aufweistbegrenztes deterministisches Chaos: Die Orbitalelemente variieren langfristig unvorhersehbar, aber die Gesamtenergie und die ersten Integrale verhindern jede makroskopische Divergenz. Mit anderen Worten: Es herrscht lokal Chaos, aber es ist soInhaltdurch die globale Topologie des Gravitationssystems.

Stabilität über Milliarden von Jahren resultiert also nicht aus der Abwesenheit von Chaos, sondern aus aKoexistenz zwischen Regelmäßigkeit und begrenzter Instabilität. Dieses fragile Gleichgewicht, das durch Resonanzen und die Massenhierarchie aufrechterhalten wird, erklärt, warum seit dem Ende der anfänglichen chaotischen Phase kein größerer Planet mehr herausgeschleudert wurde.