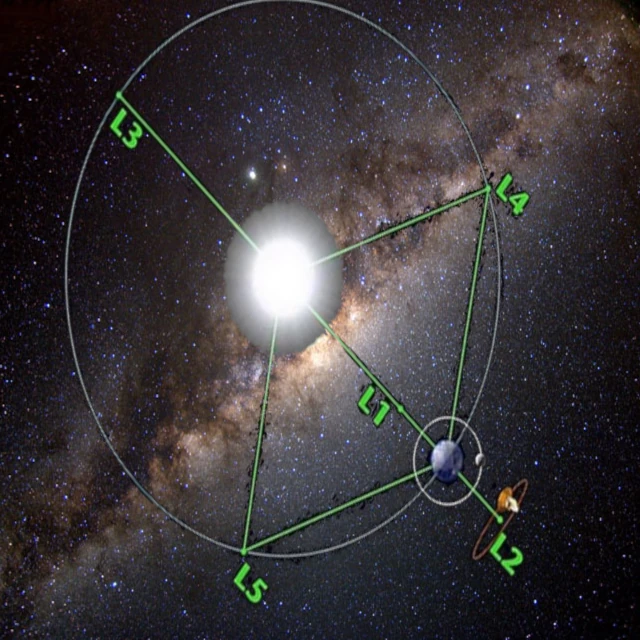
Les points de Lagrange sont cinq positions de l'espace où les forces gravitationnelles et l'effet centrifuge se compensent. Découverts mathématiquement par Joseph-Louis Lagrange (1736-1813), ils émergent de l'étude du problème restreint à trois corps. Les conditions d'équilibre s'expriment en annulant l'accélération résultante \(\vec{a} = \vec{g}_1 + \vec{g}_2 + \vec{a}_{\text{centrifuge}}\).
Le problème restreint à trois corps désigne une configuration où deux corps massifs suivent une orbite déterminée par leur gravitation mutuelle, tandis qu’un troisième corps, de masse négligeable, se déplace dans leur champ gravitationnel combiné sans perturber la dynamique des deux premiers. Cette approximation conserve les symétries essentielles du système et révèle l’existence de cinq zones d’équilibre dynamique, les points de Lagrange, dont la stabilité locale peut être analysée dans le référentiel en rotation. Elle permet de déterminer les directions stables ou instables, les fréquences de libration, sans avoir à traiter le problème général à trois corps, intrinsèquement chaotique et sans solution.
L1, L2 et L3 sont des points d’équilibre uniquement en apparence : ils sont en réalité quasi instables, si bien que la moindre perturbation (pression de radiation, variations gravitationnelles) amorce une dérive progressive.
Dans ce régime instable, une petite déviation croît naturellement jusqu’à expulser l’objet de la surface d’équilibre. Le temps caractéristique pour que cette amplification atteigne une amplitude significative est court à l’échelle orbitale : de l’ordre de quelques semaines à quelques mois, selon la masse des corps impliqués et la nature des perturbations externes.
La stabilité de L4 et L5 dépend du rapport entre les deux masses qui créent ces points d’équilibre. On définit pour cela un nombre, noté 𝜇, qui mesure « combien » la petite masse pèse par rapport au total. Si ce rapport est inférieur à une valeur critique (≈ 0,0385), alors L4 et L5 deviennent des zones quasi stables. Pour le couple Terre–Soleil, cette valeur (≈ 3 × 10-6) est très inférieure à la valeur critique. Cela explique pourquoi les points L4 et L5 du système Soleil–Terre sont stables, capables de retenir des objets comme les astéroïdes troyens.
Cependant, un objet placé près de L4 ou L5 ne reste pas immobile, il « oscille » autour du point d’équilibre, un peu comme une bille qui tourne dans un creux. Tant que ces oscillations restent petites, l’objet reste piégé dans la région, décrivant une courbe fermée en forme de « têtard », une boucle arrondie autour du point d’équilibre "la tête" et une "queue" qui s’étire le long de l’orbite principale.
L’objet quitte cette zone seulement si ses oscillations deviennent trop grandes : il franchit alors une frontière dynamique appelée « séparatrice ». Cette croissance est très lente, car elle se fait par un phénomène de diffusion chaotique : de minuscules perturbations, qui s’accumulent sur des dizaines de milliers d’orbites, finissent par agrandir progressivement l’amplitude des oscillations, jusqu’à l’éjection.
| Point | Type d’équilibre | Durée de stabilité | Sondes ou télescopes |
|---|---|---|---|
| L1 | Équilibre instable | Quelques semaines à quelques mois | SOHO (ESA/NASA, 1995) : étude du Soleil et du vent solaire ACE (NASA, 1997) : analyse du vent solaire et particules énergétiques DSCOVR (NOAA/NASA, 2015) : surveillance météorologique spatiale et vent solaire Wind (NASA, 1994) : étude plasma solaire et magnétosphère Hinode (JAXA, 2006) : observation solaire haute résolution Solar Orbiter (ESA/NASA, 2020) : images du Soleil et vent solaire polaire Parker Solar Probe (NASA, 2018) : exploration de la couronne solaire |
| L2 | Équilibre instable | Quelques semaines à quelques mois | James Webb Space Telescope (NASA/ESA/CSA, 2021) : infrarouge et cosmologie Planck (ESA, 2009-2013) : fond diffus cosmologique Herschel (ESA, 2009-2013) : observation infrarouge Gaia (ESA, 2013-) : cartographie 3D de la Voie lactée WMAP (NASA, 2001-2010) : anisotropies du fond cosmologique Euclid (ESA, prévu 2024) : énergie noire et structure à grande échelle SPICA (proposé) : mission infrarouge lointain |
| L3 | Équilibre instable | Quelques semaines à quelques mois | Aucune mission opérationnelle |
| L4 | Équilibre stable | Milliers à millions d’années | Observation des astéroïdes troyens (tel que 624 Hektor) Missions envisagées : Lucy (NASA, 2027) : étude d’astéroïdes troyens de Jupiter |
| L5 | Équilibre stable | Milliers à millions d’années | Projet Earth Trojan Survey : détection de troyens terrestres Missions futures envisagées d’étude de troyens et stabilité orbitale |
Les Points de Lagrange : L'Illusion des Oasis gravitationnelles Stables 
Némésis : La Théorie de l’Étoile Compagne du Soleil 
Système solaire vs Systèmes Stellaires : Comparaison des Systèmes Planétaires 
Le Paradoxe du Jeune Soleil Faible : Pourquoi la Terre Primitive n’était pas Gelée ? 
380 milliards de milliards de mégawatts : La Débauche d’Énergie Solaire 
L'écliptique ou l'orbite apparente du Soleil 
Maximum et minimum solaire 
Comment peser le soleil ? 
Soleil : Quand l’astre jaune devient bleu 
Explication du 8 de l'analemme 
Ligne des Glaces : la Limite qui a Façonné les Planètes 
Voyage touristique dans le système solaire 
Les Taches Solaires et le Cycle Solaire : Du Minimum au Maximum 
Le voyage infernal du photon ou marche aléatoire 
Dynamique des Cycles Solaires et Mécanismes Physiques des Éruptions Solaires 
Les grains de Baily dans une éclipse solaire 
Naissance, Vie et Mort du Soleil : Chronique d’une Étoile Moyenne 
Grains de Baily ou perles de lumière 
Lumières du Soleil et longueurs d'onde 
La formation chaotique du système solaire 
Tempêtes Solaires et Scénario Catastrophe 
Protubérances Solaires : Des Filaments de Matière dans l'Atmosphère Solaire 
Pourquoi le Soleil tourne si lentement ? Le mystère du moment cinétique manquant 
Transit de Vénus du 5 et 6 juin 2012 : Dernière Traversée Avant un Siècle 
Transit de la Lune devant le Soleil vu depuis l'espace en 2007 
Vents solaires : un phénomène clé de l’espace interplanétaire 
Héliosphère : Aux Frontières du Système Solaire
Chaos et sensibilité aux conditions initiales 
Stabilité et Chaos : Les Limites de l’Harmonie Orbitale du Système Solaire