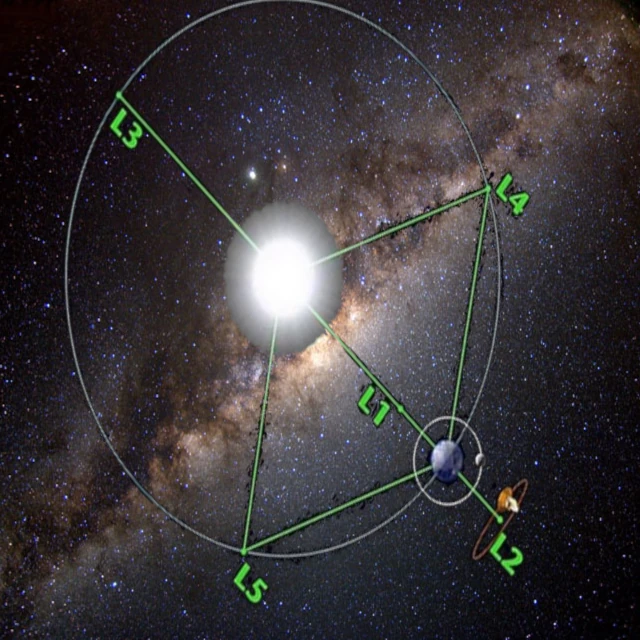
Los puntos de Lagrange son cinco posiciones en el espacio donde las fuerzas gravitacionales y el efecto centrífugo se compensan. Descubiertos matemáticamente por Joseph-Louis Lagrange (1736-1813), surgen del estudio del problema restringido de tres cuerpos. Las condiciones de equilibrio se expresan anulando la aceleración resultante \(\vec{a} = \vec{g}_1 + \vec{g}_2 + \vec{a}_{\text{centrífuga}}\).
El problema restringido de tres cuerpos designa una configuración donde dos cuerpos masivos siguen una órbita determinada por su gravitación mutua, mientras que un tercer cuerpo, de masa despreciable, se mueve en su campo gravitacional combinado sin perturbar la dinámica de los dos primeros. Esta aproximación conserva las simetrías esenciales del sistema y revela la existencia de cinco zonas de equilibrio dinámico, los puntos de Lagrange, cuya estabilidad local puede ser analizada en el referencial en rotación. Permite determinar las direcciones estables o inestables, las frecuencias de libración, sin tener que abordar el problema general de tres cuerpos, intrínsecamente caótico y sin solución.
L1, L2 y L3 son puntos de equilibrio solo en apariencia: en realidad son cuasi inestables, de modo que la más mínima perturbación (presión de radiación, variaciones gravitacionales) inicia una deriva progresiva.
En este régimen inestable, una pequeña desviación crece naturalmente hasta expulsar el objeto de la superficie de equilibrio. El tiempo característico para que esta amplificación alcance una amplitud significativa es corto a escala orbital: del orden de unas pocas semanas a unos pocos meses, dependiendo de la masa de los cuerpos involucrados y la naturaleza de las perturbaciones externas.
La estabilidad de L4 y L5 depende de la relación entre las dos masas que crean estos puntos de equilibrio. Se define para ello un número, denotado 𝜇, que mide "cuánto" pesa la masa pequeña en relación al total. Si esta relación es inferior a un valor crítico (≈ 0,0385), entonces L4 y L5 se convierten en zonas cuasi estables. Para el par Tierra-Sol, este valor (≈ 3 × 10-6) es muy inferior al valor crítico. Esto explica por qué los puntos L4 y L5 del sistema Sol-Tierra son estables, capaces de retener objetos como los asteroides troyanos.
Sin embargo, un objeto colocado cerca de L4 o L5 no permanece inmóvil, "oscila" alrededor del punto de equilibrio, un poco como una canica que gira en un hueco. Mientras estas oscilaciones permanezcan pequeñas, el objeto permanece atrapado en la región, describiendo una curva cerrada en forma de "renacuajo", un bucle redondeado alrededor del punto de equilibrio "la cabeza" y una "cola" que se extiende a lo largo de la órbita principal.
El objeto abandona esta zona solo si sus oscilaciones se vuelven demasiado grandes: entonces cruza una frontera dinámica llamada "separatriz". Este crecimiento es muy lento, ya que ocurre a través de un fenómeno de difusión caótica: pequeñas perturbaciones, que se acumulan durante decenas de miles de órbitas, terminan por aumentar gradualmente la amplitud de las oscilaciones, hasta la eyección.
| Punto | Tipo de equilibrio | Duración de estabilidad | Sondas o telescopios |
|---|---|---|---|
| L1 | Equilibrio inestable | Algunas semanas a algunos meses | SOHO (ESA/NASA, 1995): estudio del Sol y el viento solar ACE (NASA, 1997): análisis del viento solar y partículas energéticas DSCOVR (NOAA/NASA, 2015): vigilancia meteorológica espacial y viento solar Wind (NASA, 1994): estudio del plasma solar y magnetosfera Hinode (JAXA, 2006): observación solar de alta resolución Solar Orbiter (ESA/NASA, 2020): imágenes del Sol y viento solar polar Parker Solar Probe (NASA, 2018): exploración de la corona solar |
| L2 | Equilibrio inestable | Algunas semanas a algunos meses | James Webb Space Telescope (NASA/ESA/CSA, 2021): infrarrojo y cosmología Planck (ESA, 2009-2013): fondo cósmico de microondas Herschel (ESA, 2009-2013): observación infrarroja Gaia (ESA, 2013-): cartografía 3D de la Vía Láctea WMAP (NASA, 2001-2010): anisotropías del fondo cósmico Euclid (ESA, previsto 2024): energía oscura y estructura a gran escala SPICA (propuesto): misión de infrarrojo lejano |
| L3 | Equilibrio inestable | Algunas semanas a algunos meses | Ninguna misión operativa |
| L4 | Equilibrio estable | Miles a millones de años | Observación de asteroides troyanos (como 624 Hektor) Misiones previstas: Lucy (NASA, 2027): estudio de asteroides troyanos de Júpiter |
| L5 | Equilibrio estable | Miles a millones de años | Proyecto Earth Trojan Survey: detección de troyanos terrestres Misiones futuras previstas para estudiar troyanos y estabilidad orbital |
Los Puntos de Lagrange: La Ilusión de los Oasis Gravitacionales Estables 
Némesis: La Teoría de la Estrella Compañera del Sol 
Sistema Solar vs. Sistemas Estelares: Comparación de los Sistemas Planetarios 
La Paradoja del Sol Joven y Débil: ¿Por qué la Tierra Primitiva no estaba Congelada? 
380 mil millones de billones de megavatios: El Exceso de Energía Solar 
La eclíptica o la órbita aparente del Sol 
Máximo y mínimo solar 
¿Cómo pesar el
sol? 
El Sol: Cuando la Estrella Amarilla se Vuelve Azul 
Explicación del 8 del analema 
Línea de Hielo: El Límite que Moldeó los Planetas 
Viaje turístico en el sistema solar 
Las Manchas Solares y el Ciclo Solar: Del Mínimo al Máximo 
El viaje infernal del fotón o paseo aleatorio 
Dinámica de los Ciclos Solares y Mecanismos Físicos de las Llamaradas Solares 
Granos de Baily en un eclipse solar 
Nacimiento, Vida y Muerte del Sol: Crónica de una Estrella Media 
Granos de Baily o perlas de luz 
La luz del sol y las longitudes de onda 
La caótica formación del sistema solar 
Tormentas Solares y Escenario Catastrófico 
Protuberancias Solares: Filamentos de Materia en la Atmósfera Solar 
¿Por qué el Sol gira tan lentamente? El misterio del momento angular faltante 
Tránsito de Venus del 5 y 6 de junio de 2012: Último Cruce Antes de un Siglo 
Tránsito de la Luna frente al Sol visto desde el espacio en 2007 
Vientos Solares: Un Fenómeno Clave del Espacio Interplanetario 
Heliosfera: En las Fronteras del Sistema Solar
Caos y sensibilidad a las condiciones iniciales 
Estabilidad y Caos: Límites de la Armonía Orbital del Sistema Solar