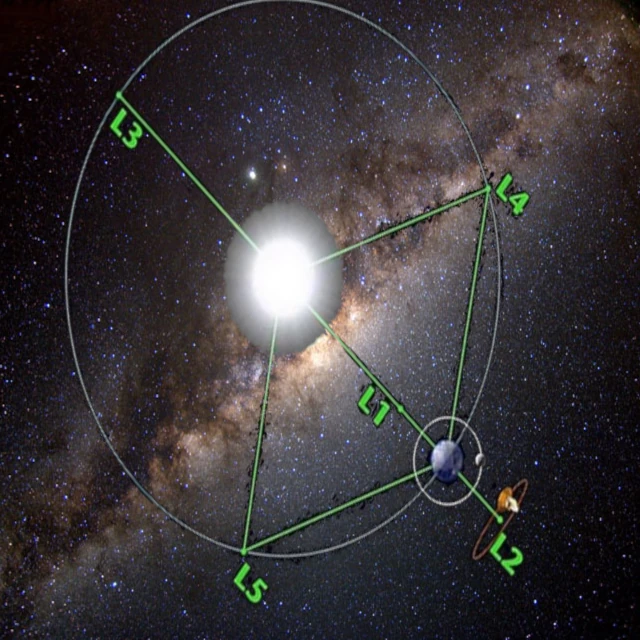
The Lagrange points are five positions in space where gravitational forces and the centrifugal effect balance each other out. Mathematically discovered by Joseph-Louis Lagrange (1736-1813), they emerge from the study of the restricted three-body problem. The equilibrium conditions are expressed by canceling the resultant acceleration \(\vec{a} = \vec{g}_1 + \vec{g}_2 + \vec{a}_{\text{centrifugal}}\).
The restricted three-body problem refers to a configuration where two massive bodies follow an orbit determined by their mutual gravitation, while a third body, of negligible mass, moves in their combined gravitational field without disturbing the dynamics of the first two. This approximation preserves the essential symmetries of the system and reveals the existence of five dynamic equilibrium zones, the Lagrange points, whose local stability can be analyzed in the rotating reference frame. It allows determining stable or unstable directions, libration frequencies, without having to address the general three-body problem, which is intrinsically chaotic and unsolvable.
L1, L2, and L3 are equilibrium points only in appearance: they are actually quasi-unstable, so that the slightest perturbation (radiation pressure, gravitational variations) initiates a gradual drift.
In this unstable regime, a small deviation naturally grows until it expels the object from the equilibrium surface. The characteristic time for this amplification to reach a significant amplitude is short on the orbital scale: on the order of a few weeks to a few months, depending on the mass of the bodies involved and the nature of external perturbations.
The stability of L4 and L5 depends on the ratio between the two masses that create these equilibrium points. A number, denoted 𝜇, is defined to measure "how much" the smaller mass weighs relative to the total. If this ratio is less than a critical value (≈ 0.0385), then L4 and L5 become quasi-stable zones. For the Earth-Sun pair, this value (≈ 3 × 10-6) is much lower than the critical value. This explains why the L4 and L5 points of the Sun-Earth system are stable, capable of retaining objects such as Trojan asteroids.
However, an object placed near L4 or L5 does not remain motionless; it "oscillates" around the equilibrium point, somewhat like a marble spinning in a hollow. As long as these oscillations remain small, the object remains trapped in the region, describing a closed curve shaped like a "tadpole," a rounded loop around the equilibrium point "the head" and a "tail" that stretches along the main orbit.
The object leaves this zone only if its oscillations become too large: it then crosses a dynamic boundary called the "separatrix." This growth is very slow, as it occurs through a chaotic diffusion phenomenon: tiny perturbations, accumulating over tens of thousands of orbits, gradually increase the amplitude of the oscillations, leading to ejection.
| Point | Type of equilibrium | Stability duration | Probes or telescopes |
|---|---|---|---|
| L1 | Unstable equilibrium | A few weeks to a few months | SOHO (ESA/NASA, 1995): study of the Sun and solar wind ACE (NASA, 1997): analysis of solar wind and energetic particles DSCOVR (NOAA/NASA, 2015): space weather monitoring and solar wind Wind (NASA, 1994): study of solar plasma and magnetosphere Hinode (JAXA, 2006): high-resolution solar observation Solar Orbiter (ESA/NASA, 2020): images of the Sun and polar solar wind Parker Solar Probe (NASA, 2018): exploration of the solar corona |
| L2 | Unstable equilibrium | A few weeks to a few months | James Webb Space Telescope (NASA/ESA/CSA, 2021): infrared and cosmology Planck (ESA, 2009-2013): cosmic microwave background Herschel (ESA, 2009-2013): infrared observation Gaia (ESA, 2013-): 3D mapping of the Milky Way WMAP (NASA, 2001-2010): anisotropies of the cosmic background Euclid (ESA, planned 2024): dark energy and large-scale structure SPICA (proposed): far-infrared mission |
| L3 | Unstable equilibrium | A few weeks to a few months | No operational mission |
| L4 | Stable equilibrium | Thousands to millions of years | Observation of Trojan asteroids (such as 624 Hektor) Planned missions: Lucy (NASA, 2027): study of Jupiter's Trojan asteroids |
| L5 | Stable equilibrium | Thousands to millions of years | Earth Trojan Survey project: detection of Earth Trojans Future missions planned to study Trojans and orbital stability |
Lagrange Points: The Illusion of Stable Gravitational Oases 
Nemesis: The Theory of the Sun's Companion Star 
Solar System vs. Stellar Systems: A Comparison of Planetary Systems 
The Faint Young Sun Paradox: Why Wasn't Early Earth Frozen? 
380 billion billion megawatts: The Solar Energy Excess 
The Ecliptic or the Apparent Orbit of the Sun 
Solar maximum and minimum 
How to weigh the sun? 
The Sun: When the Yellow Star Turns Blue 
Explanation of the 8 of the analemma 
Frost Line: The Boundary That Shaped the Planets 
Tourist trip in the solar system 
Sunspots and the Solar Cycle: From Minimum to Maximum 
The infernal journey of the photon or random walk 
Dynamics of Solar Cycles and Physical Mechanisms of Solar Flares 
Baily grains in a solar eclipse 
Birth, Life and Death of the Sun: Chronicle of an Average Star 
Grains of Baily or pearls of light 
Sunlight and wavelengths 
The chaotic formation of the solar system 
Solar Storms and Catastrophic Scenarios 
Solar Prominences: Filaments of Matter in the Solar Atmosphere 
Why Does the Sun Rotate So Slowly? The Mystery of the Missing Angular Momentum 
Venus Transit of June 5 and 6, 2012: Last Crossing Before a Century 
Transit of the Moon in front of the Sun seen from space in 2007 
Solar Winds: A Key Phenomenon of Interplanetary Space 
Heliosphere: At the Borders of the Solar System
Chaos and sensitivity to initial conditions 
Stability and Chaos: Limits of the Solar System’s Orbital Harmony