De l’Œil Nu au Télescope Spatial : Quelles sont les Méthodes pour Évaluer la Distance des Étoiles ?

Pourquoi mesurer les distances des étoiles ?

Connaître la distance des étoiles est fondamental en astrophysique. Elle permet de comprendre la structure de l'Univers et l'évolution stellaire (luminosités intrinsèques, tailles, masses, âges, etc.), d'étalonner les mesures pour établir des échelles cosmologiques, de tester les théories physiques, de rechercher des exoplanètes et la vie extraterrestre, etc.

Pour mesurer les distances des étoiles, il faut recourir à des méthodes indirectes reposant sur des principes géométriques, photométriques ou spectroscopiques.

Méthodes de mesure clés

• Parallaxe trigonométrique pour les étoiles de notre Galaxie, la Voie lactée (diamètre ~100 000 al).
• Céphéides et supernovae de type Ia (pour les galaxies).
• Décalage vers le rouge (redshift) pour les objets très lointains.

La méthode de la parallaxe stellaire : Une Géométrie à l’Échelle Cosmique

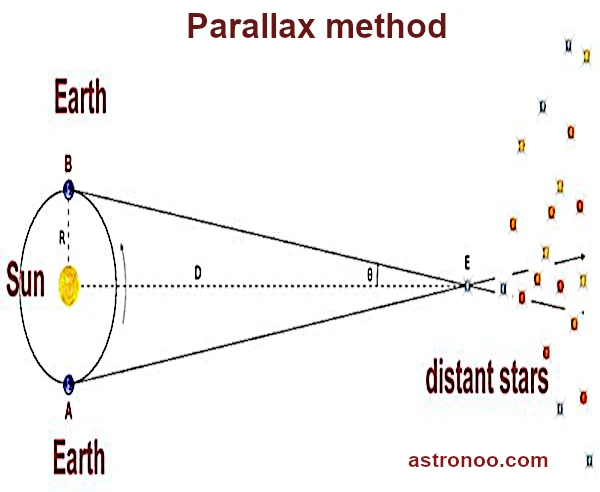
La parallaxe repose sur un principe purement géométrique : l’observation d’un astre depuis deux positions opposées de l’orbite terrestre, séparées de 6 mois, révèle un léger déplacement angulaire apparent de l’étoile par rapport au fond céleste fixe. Cet angle est appelé parallaxe annuelle \(p\) et s’exprime en secondes d’arc.

La distance \(d\) en parsecs est alors simplement donnée par la relation : \(d = \frac{1}{p}\)

où \(p\) est en secondes d’arc. Par exemple, une étoile présentant une parallaxe de \(\text{0,1}''\) est située à 10 parsecs, soit environ 32,6 années-lumière. Les satellites Hipparcos puis Gaia ont révolutionné cette méthode, permettant de mesurer des parallaxes aussi faibles que quelques microsecondes d’arc, et donc des distances de plusieurs milliers d’années-lumière.

N.B. : Avec une précision de parallaxe de 10 μas, Gaia peut mesurer des distances jusqu’à environ 326 000 années-lumière — ce qui couvre toute la Voie lactée (diamètre ~100 000 al) et même certaines galaxies satellites comme le Grand Nuage de Magellan (~160 000 al).

Les Chandelles Standards : La Photométrie des Céphéides et Supernovae

Lorsqu’un objet céleste possède une luminosité intrinsèque connue, il peut servir de « chandelle standard ». En comparant sa magnitude absolue \(M\) à sa magnitude apparente \(m\), la distance \(d\) en parsecs est obtenue via la formule du module de distance : \(m - M = 5 \log_{10}(d) - 5\)

Les étoiles variables de type céphéides sont des chandelles particulièrement précieuses : leur période de variation est directement liée à leur luminosité intrinsèque (relation période-luminosité). En mesurant leur période et leur flux reçu, on en déduit leur distance. Les supernovae de type Ia jouent un rôle similaire, mais à des échelles bien plus grandes (jusqu’à plusieurs milliards d’années-lumière).

N.B. : En 1912, Henrietta Swan Leavitt (1868–1921) a établit la relation période-luminosité des étoiles variables céphéides en étudiant les données photographiques du Petit Nuage de Magellan.

Le Décalage vers le Rouge : Le Redshift de l’Univers Observable

Pour les galaxies et objets très lointains, il n’est plus possible d’observer une parallaxe ni même des chandelles standards. On utilise alors le décalage spectral vers le rouge \(z\), conséquence de l’expansion de l’Univers. Plus une galaxie est éloignée, plus sa lumière est décalée vers le rouge.

La Loi de Hubble-Lemaître donne une estimation de la distance cosmologique, elle relie ce décalage à la distance : \(v = H_0 \cdot d\)

où \(v\) est la vitesse de récession (liée au redshift), \(H_0\) la constante de Hubble, et \(d\) la distance. Ce type de mesure permet d’explorer les confins de l’Univers observable.

Grâce à l’observation des galaxies lointaines, des quasars et du fond diffus cosmologique, on atteint des redshifts allant jusqu’à :

• z ≈ 1 → ~8 milliards d'années-lumière
• z ≈ 6 → ~12,7 milliards d'années-lumière
• z ≈ 10 → ~13,2 milliards d'années-lumière
• z = 1100 → fond diffus cosmologique, à ~13,8 milliards d’années-lumière en temps de voyage de la lumière, mais à ~46,5 milliards d’années-lumière en distance comobile (qui tient compte de l’expansion)

Méthodes additionnelles pour affiner les distances stellaires

D’autres approches sont également utilisées : les amas ouverts ou globulaires comparés à des modèles isochrones (ensemble des étoiles ayant la même âge), les étoiles de la séquence principale par photométrie multibande (ultraviolet (U), bleu (B), visible (V), rouge (R), proche infrarouge (I), etc.), ou encore l’astrosismologie (analyse des oscillations internes d’étoiles). Ces méthodes sont souvent croisées pour améliorer la précision.

Synthèse sur l’échelle des distances cosmiques

La distance des étoiles ne se mesure pas, elle se déduit. Grâce à un enchaînement de techniques imbriquées, les astronomes ont bâti une échelle cosmique, allant des étoiles proches jusqu’aux galaxies à plus de 10 milliards d’années-lumière. Chaque méthode s’appuie sur la précédente, dans un empilement hiérarchique que l’on nomme parfois la distance ladder. L’avenir, avec des instruments comme Gaia, JWST ou les futurs ELT, affinera encore cette architecture.