From the Naked Eye to the Space Telescope: What Methods Evaluate the Distance of Stars?

Why measure the distances of stars?

Knowing the distance of stars is fundamental in astrophysics. It allows us to understand the structure of the Universe and stellar evolution (intrinsic luminosities, sizes, masses, ages, etc.), to calibrate measurements to establish cosmological scales, to test physical theories, to search for exoplanets and extraterrestrial life, etc.

To measure the distances of stars, we must use indirect methods based on geometric, photometric, or spectroscopic principles.

Key measurement methods

• Trigonometric parallax for stars in our Galaxy, the Milky Way (diameter ~100,000 light-years).
• Cepheids and Type Ia supernovae (for galaxies).
• Redshift for very distant objects.

The method of stellar parallax: Geometry on a Cosmic Scale

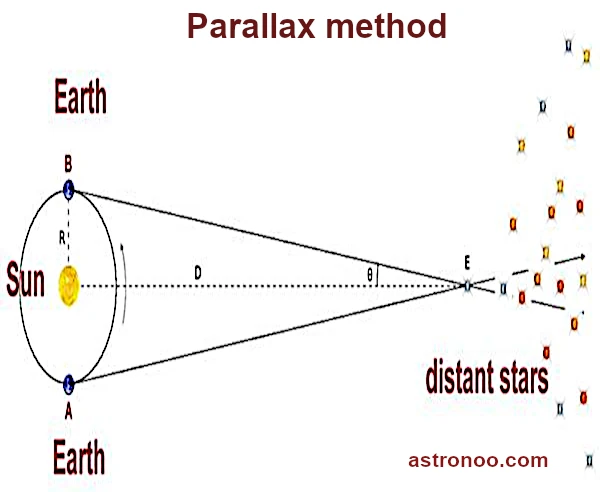
Parallax is based on a purely geometric principle: observing a star from two opposite positions in Earth's orbit, separated by 6 months, reveals a slight apparent angular displacement of the star relative to the fixed celestial background. This angle is called the annual parallax \(p\) and is expressed in arcseconds.

The distance \(d\) in parsecs is then simply given by the relation: \(d = \frac{1}{p}\)

where \(p\) is in arcseconds. For example, a star with a parallax of \(\text{0.1}''\) is located at 10 parsecs, or about 32.6 light-years. The satellites Hipparcos and then Gaia have revolutionized this method, allowing the measurement of parallaxes as small as a few microarcseconds, and thus distances of several thousand light-years.

N.B.: With a parallax precision of 10 μas, Gaia can measure distances up to about 326,000 light-years — which covers the entire Milky Way (diameter ~100,000 light-years) and even some satellite galaxies like the Large Magellanic Cloud (~160,000 light-years).

Standard Candles: Photometry of Cepheids and Supernovae

When a celestial object has a known intrinsic luminosity, it can serve as a "standard candle." By comparing its absolute magnitude \(M\) to its apparent magnitude \(m\), the distance \(d\) in parsecs is obtained via the distance modulus formula: \(m - M = 5 \log_{10}(d) - 5\)

Cepheid variable stars are particularly valuable standard candles: their period of variation is directly related to their intrinsic luminosity (period-luminosity relation). By measuring their period and received flux, we deduce their distance. Type Ia supernovae play a similar role but on much larger scales (up to several billion light-years).

N.B.: In 1912, Henrietta Swan Leavitt (1868–1921) established the period-luminosity relation of Cepheid variable stars by studying photographic data of the Small Magellanic Cloud.

Redshift: The Redshift of the Observable Universe

For very distant galaxies and objects, it is no longer possible to observe parallax or even standard candles. We then use the spectral redshift \(z\), a consequence of the expansion of the Universe. The farther a galaxy is, the more its light is redshifted.

The Hubble-Lemaître Law provides an estimate of the cosmological distance; it relates this shift to the distance: \(v = H_0 \cdot d\)

where \(v\) is the recession velocity (related to redshift), \(H_0\) is the Hubble constant, and \(d\) is the distance. This type of measurement allows us to explore the far reaches of the observable Universe.

Through the observation of distant galaxies, quasars, and the cosmic microwave background, we reach redshifts up to:

• z ≈ 1 → ~8 billion light-years
• z ≈ 6 → ~12.7 billion light-years
• z ≈ 10 → ~13.2 billion light-years
• z = 1100 → cosmic microwave background, at ~13.8 billion light-years in light travel time, but at ~46.5 billion light-years in comoving distance (which accounts for expansion)

Additional methods to refine stellar distances

Other approaches are also used: open or globular clusters compared to isochrone models (set of stars of the same age), main sequence stars by multiband photometry (ultraviolet (U), blue (B), visible (V), red (R), near-infrared (I), etc.), or astroseismology (analysis of internal oscillations of stars). These methods are often cross-referenced to improve accuracy.

Synthesis of the cosmic distance scale

The distance of stars is not measured, it is deduced. Thanks to a chain of nested techniques, astronomers have built a cosmic scale, ranging from nearby stars to galaxies more than 10 billion light-years away. Each method builds on the previous one, in a hierarchical stack sometimes called the distance ladder. The future, with instruments like Gaia, JWST, or the future ELT, will further refine this architecture.