Last updated: July 15, 2021

Where Does the Sun's Energy Come From?

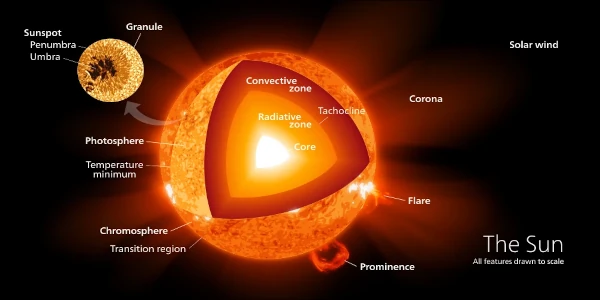
Layers of the Sun — The different layers of the Sun, including the core, the radiative zone, the convective zone, the photosphere, the chromosphere, and finally, the solar corona. At the core, the fusion of one gram of hydrogen releases as much energy as 300 tons of oil.

Energy is concentrated in the center of the Sun

The Sun is an enormous star with a diameter 109 times that of Earth, or 3.6 times the Earth-Moon distance. Its volume is 1.3 million times that of Earth.
The gravitational force at the surface (274 m/s², 28 times that of Earth) of this gigantic mass (1.989×10³⁰ kg) compresses the matter at its center. Although its core has a diameter equal to the Earth-Moon distance, the volume of the core represents only 1.5% of the total volume. It is at the core, about 15 million kelvins or degrees Celsius (1 K = -273.15 °C), that every second, 627 million tons of hydrogen fuse to produce 622.7 million tons of helium. The mass difference (4.3 million tons) is converted into energy, 4×10²⁶ joules or approximately 1.5×10¹⁹ kilowatt-hours (10 billion billion kWh).
For the past 4.57 billion years, the Sun has been consuming 4 million tons of hydrogen per second.

The gravitational pressure at the Sun's center is 26 petapascals (26×10¹⁵ Pa), or 260 billion times the atmospheric pressure at Earth's surface. At this pressure, 1 m³ of hydrogen weighs 150 tons. 1 m³ of hydrogen on Earth weighs 90 grams. So there are 1.6 million times more hydrogen atoms in 1 m³ at the Sun's center than in 1 m³ of hydrogen on Earth (not that enormous).
At this pressure and at this temperature (15 million kelvins), nuclear fusion can begin.
Hydrogen nuclei will fuse to form a helium nucleus, releasing a tremendous amount of energy (15 times more than nuclear fission triggered in our power plants).

Probability of Particle Fusion — The size or position of a proton is a probability density represented by a curve. The further from the peak of the curve, the less likely the proton’s presence or size is. However, at the bottom of the curve, the probability of two protons fusing is very low but not zero. For the nuclear reaction to "ignite," protons (hydrogen nuclei) must come into contact. Then, one of the protons transforms into a neutron. Without radioactivity, this transformation would be impossible. Two protons, even in contact, cannot overcome the Coulomb barrier; they repel each other. But a proton can transiently transform into a neutron by emitting a particle (W boson). This W boson is immediately reabsorbed, with the neutron turning back into a proton. Very rarely, the W boson decays into a positron and a neutrino, and at that moment, the neutron remains a neutron. It can then fuse with the other proton to form a deuterium nucleus and initiate the "proton-proton chain."

How to Fuse Two Protons?

For two protons to fuse, the distance between them must be extremely small, on the order of the nucleus size (10⁻¹⁵ meters). This requires overcoming the Coulomb barrier (the electric interaction force between two positively charged protons). This force is proportional to the product of the two charges and inversely proportional to the square of the distance between them (which requires considerable energy to "stick" two protons together). The closer the protons get, the more energy is needed to "stick" them together. Even at 15 million kelvins, the energy is not sufficient to overcome the Coulomb barrier. Violent collisions between protons do not crush the strong nuclear interaction bubbles enough to "stick" 2 protons together.
Theoretically, protons would need to move at 20,000 km/s to reach a temperature of 5 billion kelvins. At 15 million kelvins, protons move at 600 km/s.
However, 15 million kelvins is an average temperature. According to the Maxwell-Boltzmann distribution curve of particle velocities as a function of temperature, protons are far from reaching 20,000 km/s, making fusion impossible.
To achieve fusion, quantum physics must be invoked.
The size or position of a proton is a probability density represented by a curve. The further from the peak of the curve, the less likely the proton’s presence or size is. At the bottom of the curve, the probability of two protons fusing is very low but not zero.
The property that a quantum object can cross a potential barrier even if its energy is less than the minimum energy required to cross that barrier is called the tunneling effect.

Crossing the Coulomb barrier

Crossing the Coulomb barrier is impossible at low temperatures, but with an average of 15 million kelvins, it is enough for the tunneling effect to become probable without needing to reach 5 billion kelvins.
Every second, a proton undergoes 2×10¹⁵ collisions, and tunneling occurs once every 10⁸ collisions. Thus, each proton has 20 million opportunities to fuse.
So, why don't all the protons in the Sun fuse in one second?
Because 2 protons, even though held together by the strong nuclear interaction, cannot coexist due to Wolfgang Ernst Pauli's exclusion principle (1900–1958). Thus, each proton fuses with another proton 20 million times per second thanks to tunneling and then separates instantly (10⁻²¹ seconds).
To create a helium nucleus, it is necessary to fuse 2 protons and 2 neutrons.
Where do the neutrons come from?
The weak nuclear interaction (radioactivity) will play a role in our fusion. The weak nuclear interaction (100,000 times weaker than the strong nuclear interaction) allows a proton, with an extremely low probability (1 in 10²⁴), to transform into a neutron when in contact with another proton. When this happens, a deuterium nucleus appears, emitting a neutrino and a positron that immediately annihilates with an surrounding electron, converting matter into pure energy (E=mc²).
Deuterium will transform into helium-3, emitting pure energy (gamma rays) in the same way. With a low probability, two helium-3 nuclei will then form two helium-4 nuclei.
This process, called the "proton-proton chain," has been maintained for 4.6 billion years due to the very low probability of fusion.