最終更新日: 2025 年 8 月 29 日

近日点と遠日点: 太陽系の無望天体

頂点: 天の軌道の基本的なノード

頂点は、楕円軌道の極点を示します。重力焦点に最も近い点はと呼ばれます近点（太陽の場合は近日点）、最も遠いのは使徒（またはアフェリア）。惑星の軌道では、これらの点は軌道力学を理解する上で非常に重要です。偏心$e$ と長軸楕円の $ 2a $。距離は次の式で求められます。 $$ r_{\text{min}} = a(1 - e),\quad r_{\text{max}} = a(1 + e) $$ ここで、a は長半径です。これらの式は、離心率が大きくなるほど軌道が長くなり、近日点と遠日点の差が大きくなることがわかります。

アプシドの興味は、その性質にもあります。時間的移動性: 重力擾乱、特に惑星間の擾乱の影響下で、後尾線 (近日点と遠日点を結ぶ線) が先行するつまり、軌道面内でゆっくりと回転します。一般相対性理論によって説明される水星の近日点の前進によって示されるように、この歳差運動は非ニュートン効果の敏感な指標です。

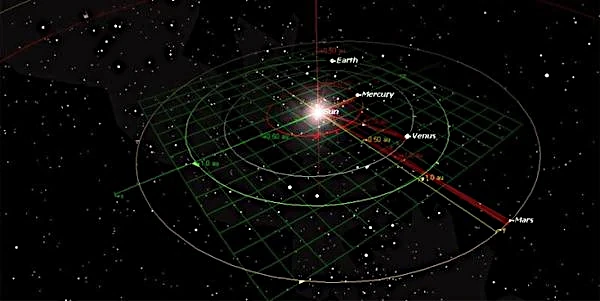
太陽系の内部軌道

内惑星 (水星、金星、地球、火星) は太陽に比較的近い軌道を持っているため、潮汐作用や太陽風との相互作用が強化されます。それらの遠辺は、現代の天体暦を使用して非常に正確に測定されます。水星は離心率 $e \約 0.206$ が高く、非常に楕円形の軌道を持っています。近日点は 4,600 万 km、遠日点は 7,000 万 km です。この不均衡により、太陽付近の 59 km/s から遠日点の約 39 km/s まで、非常に変動する軌道速度が発生します。

水星の近日点歳差運動は象徴的な現象です。ニュートンの法則は、他の惑星からの擾乱による一定の進歩を予測していますが、観測では 1 世紀あたり 43 インチ (秒角) を超える超過が示されており、これはアインシュタインの形式主義における時空の湾曲によって完全に説明されます。

地球は、円に近い軌道 $e \約 0.0167$ を持ち、近日点 (1 億 4,710 万 km) と遠日点 (1 億 5,210 万 km) の間にわずかな変動があります。この違いは、受け取る太陽エネルギーの量に影響します（太陽定数は約 6% 変化します）が、23.5 度の軸傾きに依存する季節の主な原因ではありません。

より遠い火星の離心率は 0.093 で、地球のほぼ 6 倍です。その近日点 (2 億 600 万 km) と遠日点 (2 億 4,900 万 km) では、季節変動がより強調されており、特に半球間の非対称な気候で顕著です。

金星の場合は興味深い例で、その軌道はほぼ完全な円形 $e \約 0.0068$ です。その結果、頂点間の変動は無視できますが、ノードを通過するときに位置合わせが正確であれば、地球から観察されるトランジットにおいて重要な役割を果たします。

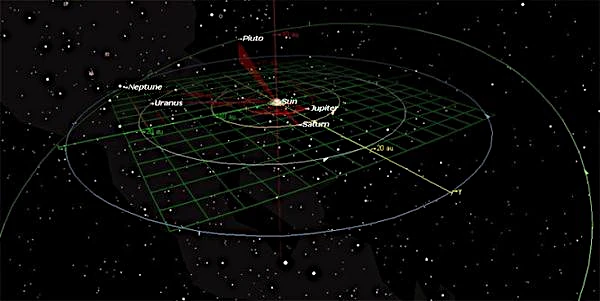
太陽系の外側の軌道

外側の惑星 (木星から海王星) は、内側の惑星よりも幅が広く、一般的により円形の軌道を描きます。ただし、彼らは経験します重力共鳴相互に、ゆっくりと頂点を修正します。支配的な巨人である木星は、太陽系の構造に強い影響を与えます。近日点は 7 億 4,000 万 km、遠日点は 8 億 1,600 万 km で、離心率は中程度 $ e \約 0.049 $ です。

土星、天王星、海王星は、平均距離に比べて後天体の偏差が比較的小さい (数千万 km) ため、長期的には動きがより安定します。しかし、それらの軌道は、環の分光分析や衛星の追跡によって検出される、遠望点線のゆっくりとした歳差運動にも影響されます。

海王星横断天体はさらに極端な偏心性を示します。 $e \約 0.2488$ の冥王星は、近日点か遠日点かに応じて 44 億 km から 73 億 km まで移動します。この変動により、冥王星が一時的に海王星よりも太陽に近づく可能性があります。その頂面の線は傾斜しており (約 17°)、非常に可動性があり、混沌とした体制を反映しています。

エリス、セドナ、オールトの雲の極端な天体などの他の遠方の天体は、500 天文単位を超える遠方に到達します。たとえば、セドナは離心率の高い軌道 $e \およそ 0{,}854$ を持ち、近日点は 76 天文単位、遠日点は 937 天文単位と推定されています。これらの天体は過去の擾乱の化石証人であり、おそらく近くの星やまだ検出されていない仮説上の惑星と関係があると考えられます。

これらの遠く離れた後陣は、太陽系の境界とそこに支配する重力を理解するために不可欠です。特に相対論的効果、共鳴、銀河潮汐を考慮する場合、それらの軌道は単純な分析方法では説明できないため、数値シミュレーションによって研究されます。