肉眼から宇宙望遠鏡まで: 星の距離を評価する方法は何ですか?

なぜ星の距離を測定するのでしょうか?

星までの距離を知ることは天体物理学の基礎です。これにより、宇宙の構造と星の進化 (固有光度、サイズ、質量、年齢など) を理解し、宇宙論的スケールを確立するための測定値の校正、物理理論のテスト、系外惑星や地球外生命体の探索などが可能になります。

星の距離を測定するには、幾何学、測光、または分光学の原理に基づいた間接的な方法を使用する必要があります。

主な測定方法

• 私たちの銀河系、天の川銀河（直径約 100,000 ライ）の星々の三角視差。
• セファイドと Ia 型超新星 (銀河の場合)。
• 非常に遠いオブジェクトの赤方偏移。

恒星視差法: 宇宙スケールの幾何学

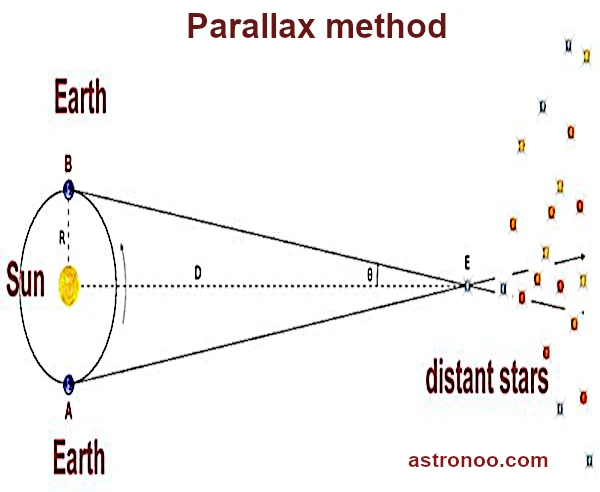
視差は純粋に幾何学的原理に基づいています。地球の軌道上の 6 か月離れた 2 つの反対側の位置から星を観察すると、固定された天の背景に対する星のわずかな見かけの角変位が明らかになります。 この角度は年周視差 \(p\) と呼ばれ、弧の秒数で表されます。

パーセク単位の距離 \(d\) は、次の関係式で単純に求められます: \(d = \frac{1}{p}\)

ここで、 \(p\) の単位は秒角です。たとえば、\(\text{0,1}''\) の視差を持つ星は 10 パーセク、つまり約 32.6 光年離れたところにあります。衛星ヒッパルコスそれからガイアはこの方法に革命をもたらし、数マイクロ秒という小さな視差、つまり数千光年の距離の測定を可能にしました。

注： :
視差精度10μasで、ガイア約 326,000 光年までの距離を測定できます。これは、天の川銀河全体 (直径約 100,000 年) と、大マゼラン雲 (約 160,000 年) のような一部の衛星銀河さえもカバーします。

標準キャンドル: セファイドと超新星の測光

天体が既知の固有光度を持っている場合、それは「標準キャンドル」として機能します。絶対等級 \(M\) と見かけの等級 \(m\) を比較すると、距離係数の公式 \(m - M = 5 \log_{10}(d) - 5\) を介してパーセク単位の距離 \(d\) が得られます。

セファイド型変光星は特に貴重なろうそくであり、その変動周期はその固有光度に直接関係しています (周期と光度の関係)。それらの周期と受信磁束を測定することで、それらの距離を推定します。 Ia 型超新星も同様の役割を果たしますが、その規模ははるかに大きくなります (最大数十億光年)。

注： :
1912年に、ヘンリエッタ・スワン・リービット(1868–1921) は、小マゼラン雲の写真データを研究することにより、セファイド変光星の周期と光度の関係を確立しました。

赤方偏移: 観測可能な宇宙の赤方偏移

非常に遠い銀河や天体については、視差や標準的なろうそくでさえ観察することはもはや不可能です。次に、宇宙の膨張の結果であるスペクトル赤方偏移 \(z\) を使用します。銀河が遠くになるほど、その光の赤方偏移は大きくなります。

そこにはハッブル・ルメートルの法則宇宙論的距離の推定値を与えると、このシフトを距離に関連付けます: \(v = H_0 \cdot d\)

ここで、 \(v\) は後退速度 (赤方偏移に関連)、 \(H_0\) はハッブル定数、 \(d\) は距離です。このタイプの測定により、観測可能な宇宙の限界を探索することが可能になります。

遠方の銀河、クエーサー、宇宙マイクロ波背景放射の観測のおかげで、私たちは最大で次のような赤方偏移を達成しています。

• z ≈ 1 → 約80億光年
• z ≈ 6 → ~127 億光年
• z ≈ 10 → ~132 億光年
• z = 1100 → 宇宙マイクロ波背景、光の移動時間では約 138 億光年離れていますが、移動距離では約 465 億光年離れています (膨張を考慮)

恒星間距離を精緻化するための追加の方法

その他のアプローチも使用されます。等時性モデル (同じ年齢の星のセット) と比較した散開星団または球状星団、マルチバンド測光法 (紫外 (U)、青 (B)、可視光 (V)、赤 (R)、近赤外 (I) など) による主系列星、さらには天体地震学 (星の内部振動の分析) です。精度を向上させるために、これらの方法が頻繁に使用されます。

宇宙の距離のスケールに関するまとめ

星の距離は測定できませんが、推測されます。一連の連動技術のおかげで、天文学者は近くの星から 100 億光年以上離れた銀河に至るまでの宇宙規模を構築しました。各メソッドは、階層スタック内で前のメソッドに基づいて構築されます。距離はしご。将来、Gaia、JWST、または将来の ELT などの機器を使用して、このアーキテクチャはさらに洗練されるでしょう。