E=mc²: One Equation, One Revolution

Special Relativity: Much More Than a Famous Formula

E=mc² is the most well-known and popularized equation in all of physics.

The equation E=mc² first appeared in Albert Einstein's article titled "Does the Inertia of a Body Depend Upon Its Energy Content?", published in the journal Annalen der Physik on September 27, 1905. It appeared after the article of June 30, 1905, titled "On the Electrodynamics of Moving Bodies". This June 1905 article contains the basis of what will later be called "The Theory of Special Relativity".

The theory of special relativity is based on two principles: Galilean relativity and the invariance of the speed of light. Galilean relativity states that the laws of physics remain unchanged in inertial frames of reference (reference systems in uniform motion), now called Galilean frames. Moreover, speed is relative to a reference point, an arbitrarily chosen point as fixed. The invariance of the speed of light implies that it is a limiting and unsurpassable speed, regardless of the reference frame.

But what exactly does the equation E=mc² mean?

In reality, the original equation is E²=m²c⁴+p²c² (E=energy, m=mass, c=speed of light, p=momentum). In other words, the total energy of a body is the sum of its rest mass energy (m²c⁴) plus its kinetic energy (p²c²).

If a body is stationary, its momentum is zero, then E²=m²c⁴ ⇒ E=mc². Other forms of the equation are m=E/c² or Δm=ΔE/c² (Δ=variation).

This equation E=mc² has enormous consequences on the concepts of space, time, mass, and energy, as well as on the physics of the infinitely large (cosmology) and the infinitely small (quantum physics).

Note: Law of composition of velocities: If V1 is the velocity of the reference frame R1 (for example, a train traveling at 100 km/h) and V2 is the velocity of a walker (reference frame R2) who moves at 10 km/h in the same direction as the train relative to the train, at what velocity V0 does the walker move relative to the platform (reference frame R0)? The answer is V0 = V1+V2=110 km/h. From the platform's point of view, the train is moving at 100 km/h and the walker at 110 km/h. From the train's point of view, the walker is moving at 10 km/h and the platform at -100 km/h. From the walker's point of view, the train is moving at -10 km/h and the platform at -110 km/h. Velocity is relative; it depends on the point of view. No mechanical experiment inside the inertial reference frame can determine the velocity of its own reference frame.

Note: The momentum or the amount of motion transmitted to an object is the product of mass by velocity (p=mv). This corresponds to the inertia of the object or the difficulty in changing its motion.

Luminiferous Aether: When Light Traveled in the Aether

In the article of June 30, 1905, published in Annalen der Physik "On the Electrodynamics of Moving Bodies", Einstein postulates that light is not only wave-like but also consists of photons (light corpuscles). This will allow him to challenge the existence of the aether.

Light, redefined by Maxwell, has been considered since the 17th century as a wave. Sound needs a medium (air) that vibrates as the sound passes. Similarly, a wave needs a medium (water) to propagate. Physicists of the 18th century then invented the luminiferous aether, an immaterial substrate that serves as a support in the vacuum to carry light. The aether vibrating as light passes was a consensus in the scientific world. For Einstein, if light is not only wave-like but also consists of photons, then there is no need for luminiferous aether.

Einstein strongly rejected the stationary nature of the aether defended by Lorentz because it was contrary to the principle of relativity. Light can propagate in a vacuum as corpuscles.

Note: According to the equations of James Clerk Maxwell (1831-1879), light is a self-propagating transverse electromagnetic wave with electric and magnetic components where the electric and magnetic fields oscillate at right angles to each other and propagate perpendicular to the direction in which they are moving indefinitely unless absorbed by intervening matter. In other words, each type of field—electric and magnetic—generates the other to propagate the entire composite structure in empty space at the finite speed of light, c (from the Latin celeritas "speed").

Speed of Light: The Ultimate Limit of Nature

The elimination of the aether tells us that the notion of absolute velocity does not exist; velocity is relative. This implies that if an object has a velocity c in one reference frame, then it has a velocity c in all reference frames.

How to accept this oddity?

The following postulates are necessary to understand the theory of special relativity.

• There is no privileged point in space and time; spacetime is homogeneous. If an experiment is conducted, the measurements will remain valid here and there, yesterday and tomorrow.
• There is no privileged direction in space (space is isotropic). If an experiment is conducted, the measurements will remain valid in all directions of space, unlike time, which always goes in the same direction (from past to future).
• The same transformation laws relate the measurements of experiments seen by observers located in different inertial reference frames.
• If an event A is the cause of an event B, regardless of the observer, event A will always be the cause of event B. Causality must be respected, meaning the order of events will never be reversed regardless of the motion.

If we accept these postulates, the Lorentz transformations (1853-1928) modify the law of composition of velocities.

V=V1+V2 becomes V=(V1+V2)/(1 + V1V2/c²)

It is demonstrated that if V2=c ⇒ V=c. The energy of V2 being maximal, the velocity V1 is zero!

V=(V1+c)/(1+V1c/c²)=(V1+c)/(1+V1/c)=c(V1+c)/(c+V1)=c

c has become a limiting constant, and objects moving at velocity c do not depend on the reference frame. If an object propagates at the speed of light, then it will propagate at the speed of light for all observers. The experiment gives c=299,792,458 m/s. At our scale, V1 and V2 are small compared to c, so the Lorentz factor (γ=1/√(1-v²/c²)) very close to 1 allows us to find V≈V1+V2.

The Lorentz factor is the proportionality factor by which relativistic time, lengths, and mass change for an object while it is in motion. This factor takes an infinite value when the object's velocity reaches the speed of light.

γ=1/√(1-v²/c²) ⇒ γ=1/√(1-c²/c²) ⇒ γ=1/0 = ∞

The graph of the Lorentz factor shows an asymptote. This asymptote rises sharply vertically as v approaches c. Here are some values of the Lorentz factor corresponding to different velocity values.

• At 10% of c, the factor γ=1.005
• At 20% of c, the factor γ=1.021
• At 50% of c, the factor γ=1.16
• At 99% of c, the factor γ≈7
• At 99.9% of c, the factor γ≈22
• At 99.99% of c, the factor γ≈71
• At 100% of c, the gamma factor is infinite.

Time Dilation: The Impact of Velocity and Gravity

The Lorentz factor (γ=1/√(1-v²/c²)) applies to all concepts in a relativistic framework, and of course, time is concerned.

A laser beam reflecting off the Moon takes 1.3 seconds to go and 1.3 seconds to return. The back-and-forth motion of the laser beam traveling between two mirrors can be considered a clock. A pilot passing at very high speed next to the Earth observes a strange phenomenon. He sees the light moving in a round trip not vertically but in a zigzag. The beam travels a longer distance for him than for an observer on Earth. The direction of the laser seen by the observer on the ground is vertical, so the distance is shorter than that seen by the pilot.

Since v=dt and the speed of light is invariant, if v is invariant and the distance d is greater, then time is shorter. From the pilot's point of view, the light pendulum oscillates more slowly than for the observer on Earth.

In the spacecraft, time dilates by a factor γ, which is a function of the spacecraft's velocity. Motion causes a slowdown of time. This has been demonstrated practically with atomic clocks that allow extremely precise measurements. Two atomic clocks, one installed in a flying airplane and the other placed on the ground, obtain different time measurements. There is a desynchronization of the clocks. The airplane's clock is slower by a few nanoseconds, but the difference is real and measurable. This tiny difference is due to the airplane's low speed compared to the speed of light.

Length Contraction: A Fundamental Relativistic Effect

The Lorentz factor (γ=1/√(1-v²/c²)) applies to all concepts in a relativistic framework. Lengths are also concerned.

To measure the length of a moving object, its endpoints must be measured simultaneously (at exactly the same moment). This is not possible for an object traveling at the speed of light. To measure it, it must be stationary. Therefore, one must be in its own reference frame where the object is stationary.

In its reference frame, the length of moving objects is reduced by a factor gamma. To understand this phenomenon of length contraction, an example will be more explicit than equations.

Muons are elementary particles with a negative electric charge, unstable, produced in the upper atmosphere at an altitude of 35 km. Cosmic rays are fluxes of atomic nuclei (protons) of high relativistic energy, coming from space. When cosmic rays collide with oxygen or nitrogen atoms in the upper atmosphere, they produce showers of particles, including muons. Muons have a lifespan of 2.2 μs on average and travel at a speed very close to that of light. This means that during their entire lifetime, they travel only an average of 660 meters.

How is it possible to find muons on the ground (35 km lower) when they can only travel 660 m?

Muons have a lot of energy, so the time dilation effect described by special relativity makes them observable on the Earth's surface.

Indeed, from the ground observer's point of view, the lifespan of the muon moving at the speed of light is dilated by a factor γ (2.2 γ). From its point of view, the muon will live 75 times longer, and it will be possible to find it on the ground. From the muon's point of view, it is the Earth that is moving towards it at the speed of light. It will see the size of the Earth reduced by the same factor γ. For the muon, the 35 km of the atmosphere will be only 660 m, and it will be able to reach the ground before disappearing.

Both points of view lead to the same physical result. From the ground observer's point of view, there is time dilation. From the muon's point of view, there is length contraction. Just like with time dilation, we do not observe length contraction in our daily lives because our travel speeds are very low compared to the speed of light.

Mass: From Theory to Practice

In E=mc², the enormity of the factor c² tells us that an object possesses a gigantic amount of energy solely by virtue of its mass.

• If we could extract all the energy contained in 1 gram of matter, we would obtain 90,000 GJ [E=0.001x(3x10⁸)²=9x10¹³ joules] or 25 GWh, which is the daily production of a 1 GW nuclear power plant. The mass energy contained in 1 mg of matter is equal to the chemical energy of 2 tons of oil (1 ton of oil = 41.868 GJ). The mass energy hidden from us is truly gigantic!!!
• A massive body emits electromagnetic radiation, hence light (visible especially when heating a metal). A massive body loses mass as soon as it loses energy. In other words, a body can lose mass without losing particles. This means that mass no longer measures the amount of matter in a body but its amount of energy. For example, the mass of a hydrogen nucleus is not equal to the sum of the mass of the proton plus that of the electron. When the proton and electron are bound, the nucleus tends towards a parsimonious ground state (lowest potential energy). To reach this ground state, an amount of energy ΔE is released, thus the energy of the system decreases. By losing this extremely small amount of energy, the nucleus also loses mass (ΔE=Δmc²). Conversely, when the atom regains energy, the system increases its mass. This is valid for all atoms of matter. For example, the mass of the helium nucleus (2 protons + 2 neutrons) = 6.646 yg (1 yoctogram = 10⁻²⁴ grams). The mass of the proton = 1.673 yg. The mass of the neutron = 1.675 yg. The mass of the 2 protons + the mass of the 2 neutrons = 6.696 yg. It is observed that the mass of the nucleus is less than the mass of its constituents. When protons and neutrons bind together, the mass of the system decreases by 1% Δm=ΔE/c² (lowest potential energy). A ΔE is released. This is not huge, but this nuclear fusion energy allows stars to shine.
• The mass of a proton (2 up quarks + 1 down quark) is 1.673 yg or 1.673x10⁻²⁴ g. The mass of a neutron (1 up quark + 2 down quarks) is 1.675 yg. The mass of an up quark is 0.004 yg. The mass of a down quark is 0.009 yg.

Why does the mass of quarks represent only about 2 thousandths of the mass of nucleons?

The kinetic energy and the strong interaction energy agitate and hold the quarks together. This means that mass contains only energy. The profound nature of mass is the energy due to the frenetic dance of elementary particles.

• If a particle that emits light has no mass (m²c⁴=E²-p²c²), then its total energy is equal to its kinetic energy (E²-p²c² ⇒ E=pc). Thus, mass is equal to inertia as in Newton's equations (f=ma and f=mv).
• If a particle is not at rest, momentum must be added (E²=m²c⁴+p²c²), thus special relativity allows the existence of massless particles. A particle can have energy without having mass; it is sufficient for its momentum to be non-zero. This is the case for photons. Massless particles cannot be at rest; they are forced to travel at the speed of light.
• If a particle has a velocity equal to c, its energy is maximal; consequently, its mass is zero m²c⁴=E²-p²c²=0.
• Mass is converted into energy (m=E/c² or Δm=ΔE/c²) in the production of nuclear energy. Very heavy atomic nuclei (uranium-235, plutonium-239) contain a lot of protons and are unstable. If one of these atoms captures a neutron, it transforms into an even more unstable nucleus (²³⁶U or ²⁴⁰Pu) and gains energy. The resulting nucleus splits into two nuclei and then releases two or three neutrons available for other nuclear fissions (principle of the chain reaction).

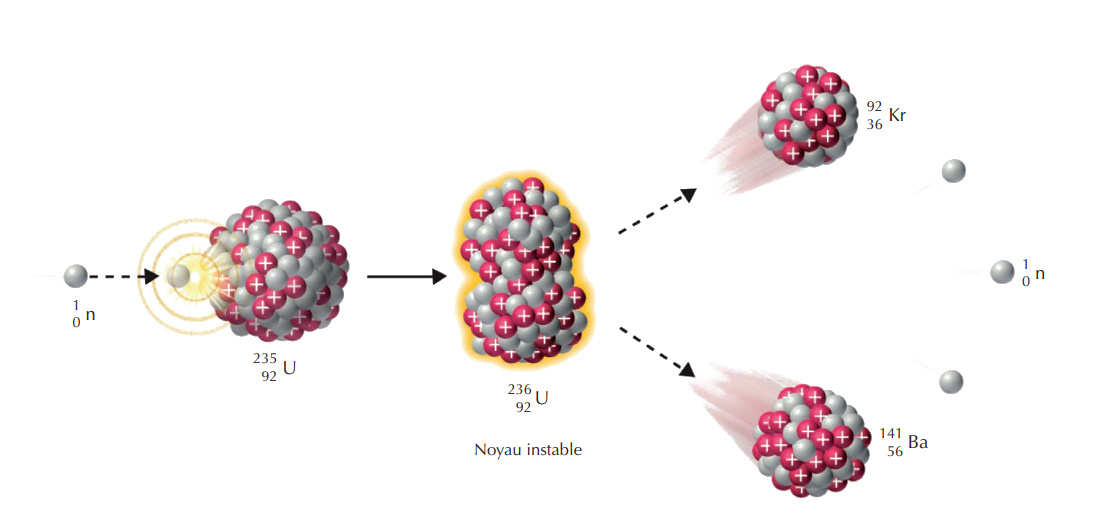
In this reaction, the mass of the two nuclei plus the mass of the released neutrons is less than the mass of the initial uranium-235 nucleus. Mass has been converted into kinetic energy. It is this energy produced by fission that we will recover. The fission of a uranium-235 atom releases approximately 193.2 MeV of recoverable energy. The energy released by nuclear fuels is a million times greater than that of chemical fossil fuels.

• Chemical reactions also convert mass into energy but at a much lower level, on the order of one billionth.

Energy: The Evolution of the Concept of Energy

The Lorentz factor (γ=1/√(1-v²/c²)) applies to all concepts in a relativistic framework, and of course, energy is concerned.

• In the equation E=mc²/√(1-v²/c²)-mc², if the velocity of the body is very small compared to the speed of light (up to 100,000 km/s), we find the macroscopic world's kinetic energy Ec=mc²/√(1-v²/c²)-mc² ⇒ ½mv².
• If the velocity approaches the speed of light, the kinetic energy tends towards infinity. This means that it is not possible to exceed the speed of light because to give an object a velocity equal to c, an infinite amount of energy would be required, Ec=∞, which is impossible. In other words, the more massive a body is, the greater its resistance to motion. The faster it moves, the harder it is to change its motion. We gradually reach a limiting speed that cannot be exceeded. At that point, the inertia is so high that all the energy in the universe would not be enough to make it go faster. We understand why the speed of light is a limiting speed in the entire observable universe.
• Ec=mc²/√(1-v²/c²)-mc² in this equation, kinetic energy is converted into mass, which is what we do in particle accelerators.

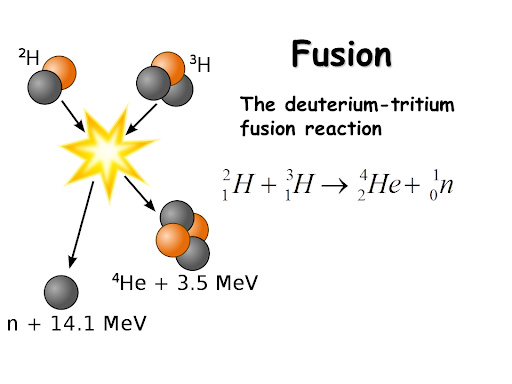
High-energy particle beams circulating in opposite directions and colliding cause the appearance of a very large number of particles that are detected using high-energy particle detectors. When we measure the total mass of all the particles created by the collision and compare it to the mass of the initial particles, we find a value up to 200,000 times higher. In other words, mass is not conserved, and the kinetic energy of the initial particles has materialized. It has transformed into new particles. Kinetic energy has transformed into mass!

• Δm=ΔE/c², in thermonuclear fusion, mass is converted into energy. A positively charged deuterium nucleus or tritium nucleus cannot naturally bind. But in the tokamak, under the influence of extreme temperature and pressure, hydrogen atoms can fuse and generate energy. The mass balance shows that the mass after the fusion reaction is smaller than the mass before the reaction. The difference in mass has been transformed into energy.

Antimatter: A Hidden Reality of Our Universe

Antimatter is also a consequence of the equation E=mc². Matter and antimatter, upon meeting, annihilate and transform 100% of their mass into pure energy.

• For example, an electron (negative) and a positron (positive) can fuse and transform into very high-energy gamma photons. Thus, the conversion of matter into energy is total.

Every time a particle meets an antiparticle, it annihilates instantly into pure energy, as in the functional imaging technique of nuclear medicine used in PET (positron emission tomography). A radioactive isotope (fluorine-18) in a microdose incorporated into a "precursor" molecule is injected into the patient. The product will diffuse into the organs, and from time to time, the ¹⁸F-fluoro-deoxy-D-glucose (¹⁸FDG) will decay, emitting positrons. In the presence of nearby electrons, these positrons will decay, emitting beta radiation. These photons will pass through the patient's body and be detected by the machine. We can thus determine where the glucose has gone.

The isotopes most commonly used in PET imaging have a generally short radioactive half-life (time required for half of the radioactivity to decay). Consequently, radiotracers are produced by a cyclotron a few hours before their use. Positron emission tomography is a technique that uses antimatter.

Note: Beta radiation is a form of radioactivity in which a nucleus emits an electron and an antineutrino (beta-minus radiation) or a positron and a neutrino (beta-plus radiation). This process gives rise to another nucleus having one fewer neutron and one more proton than the initial nucleus.

Spacetime: A New Perspective on the Universe

Spacetime emerged with special relativity, and its geometric representation was taken up by Hermann Minkowski (1864-1909) in 1908.

The spacetime continuum has four dimensions. Three dimensions for space (x, y, z) and one for time (ct), which is transformed into a distance by associating it with the constant c (d=ct). In spacetime, time is geometrized, allowing all events to be positioned in time and space by their coordinates ct, x, y, z, all of which depend on the reference frame because time does not unfold in the same way depending on the reference frame.

The measurement of time, transformed into a measurement of distance, can be associated with the other three coordinates of space. Thus, all measurements are in units of distance. Time has become space!

All point events are connected at the speed of light. The set of all events is called "spacetime." The boundary defined by the light cone is called the "cosmological horizon."

The world lines defining the cone can be described by a particle moving at the speed of light, which defines the boundary of the cone. The representation of the world lines in the lower part (inverted cone) comes from the fact that an event can also have a past. If the object is stationary in spacetime, it does not move in space but moves in time (vertical axis).

If the object is in motion, necessarily at a speed less than c, the displacement will take place inside the light cone having the origin as its apex (the present). The world line of a moving character has an angle in the cone that depends on its velocity; it moves in space and time. The edges of the cone define the limiting speed, that of light particles. The surface of the cone is reserved for the representation of the propagation of light signals emitted by the object.

The interior of the upper light cone (positive side) represents "the future." The apex of the light cone represents "here and now." The interior of the lower light cone (negative side) represents "the past." The exterior of the cone is not accessible by a light signal because it would go faster than the speed of light. The exterior represents "elsewhere."

A real-world body has a world line in spacetime. The set of its history (all the events of its life) traces this line. In Minkowski's four-dimensional Euclidean universe, the trajectories of objects in spacetime are always straight lines.

Key Takeaways

Understanding special relativity is far from immediate; it requires a lot of imagination to grasp the concepts hidden behind the equation E=mc². Many physicists contributed to the emergence of this formula in Einstein's mind.

• Galileo (1564-1642) for Galilean relativity and the reference system in uniform motion.
• Isaac Newton (1642-1727) for his laws of motion.
• Michael Faraday (1791-1867) for his work on electricity and magnetism.
• James Clerk Maxwell (1831-1879) for unifying electricity and magnetism and integrating light into the electromagnetic phenomenon.
• George Fitzgerald (1851-1901) for length contraction.
• Hendrik Antoon Lorentz (1853-1928) for length contraction and time dilation.
• Henri Poincaré (1854-1912) for the group structure of Lorentz transformations.
• Albert Abraham Michelson (1852-1931) and Edward Williams Morley (1838-1923) for the experiment on the invariance of the speed of light in the luminiferous aether.

• For Einstein, light consists of photons; there is no need for luminiferous aether.
• There is a limiting speed that objects cannot exceed. This speed links mass and energy.
• c is no longer the speed of a massless object but becomes a universal constant of physics that we find in all phenomena.
• At the speed of light, time no longer flows. There is no zero speed; there is no absolute reference frame. The idea of immobility does not exist.
• The simple application of the Lorentz factor explains the invariance of the speed of light and its limit, time dilation, and length contraction.
• Energy and matter are of the same nature. For energy to become mass, a lot of energy is needed; for mass to become energy, very little mass is needed. The mass of a body represents the energy container.
• Matter and antimatter, upon meeting, annihilate and transform 100% of their mass into pure energy.
• The spacetime continuum has four dimensions. Three dimensions for space (x, y, z) and one for time (ct), which is transformed into a distance by associating it with the constant c (d=ct). In spacetime, time is geometrized.
• With this mysterious formula E=mc² that defies common sense, Albert Einstein put the entire universe into an equation, from the infinitely large to the infinitely small. E=mc² unites cosmology and quantum physics. If this equation were proven wrong, all of our physics would collapse.