
Desde principios del siglo XX, la noción de tiempo dejó de ser un simple parámetro universal, presente desde siempre, para convertirse en una dimensión integrada en la estructura misma del Universo. La teoría de la relatividad especial, formulada en 1905 por Albert Einstein (1879-1955), mostró que la duración medida depende del movimiento relativo del observador. En 1915, la relatividad general introdujo la curvatura del espacio-tiempo bajo el efecto de la masa y la energía.
El espacio-tiempo puede describirse como una variedad de cuatro dimensiones donde los eventos tienen coordenadas \((x, y, z, ct)\). La métrica de Minkowski, que formaliza el intervalo espacio-temporal de la relatividad especial, fue formulada en 1908 por Hermann Minkowski (1864-1909).
Define el intervalo invariante: $$ \boxed{\color{blue}{\displaystyle s^2}} = (ct)^2 - x^2 - y^2 - z^2 $$
Esta relación muestra que el tiempo y el espacio están íntimamente ligados, y que la geometría del tiempo depende de la velocidad del observador y de la gravitación.
A menudo se escriben las coordenadas de un evento como (x, y, z, ct) en lugar de (x, y, z, t) para que el componente temporal ct tenga la misma dimensión (longitud) que las coordenadas espaciales.
Problema: x, y y z se expresan en metros, mientras que ���� se expresa en segundos → Imposible sumarlos directamente en una norma o distancia.
Solución: Multiplicar ���� por ���� (velocidad de la luz), que tiene la unidad m/s: ��������[m]. Así, ct está en metros, como x, y, z. Esta homogeneidad hace que el intervalo de Minkowski, \( \boldsymbol{s^2} = (ct)^2 - x^2 - y^2 - z^2 \), sea más compacto y permite representar el espacio y el tiempo en un mismo marco geométrico de cuatro dimensiones.
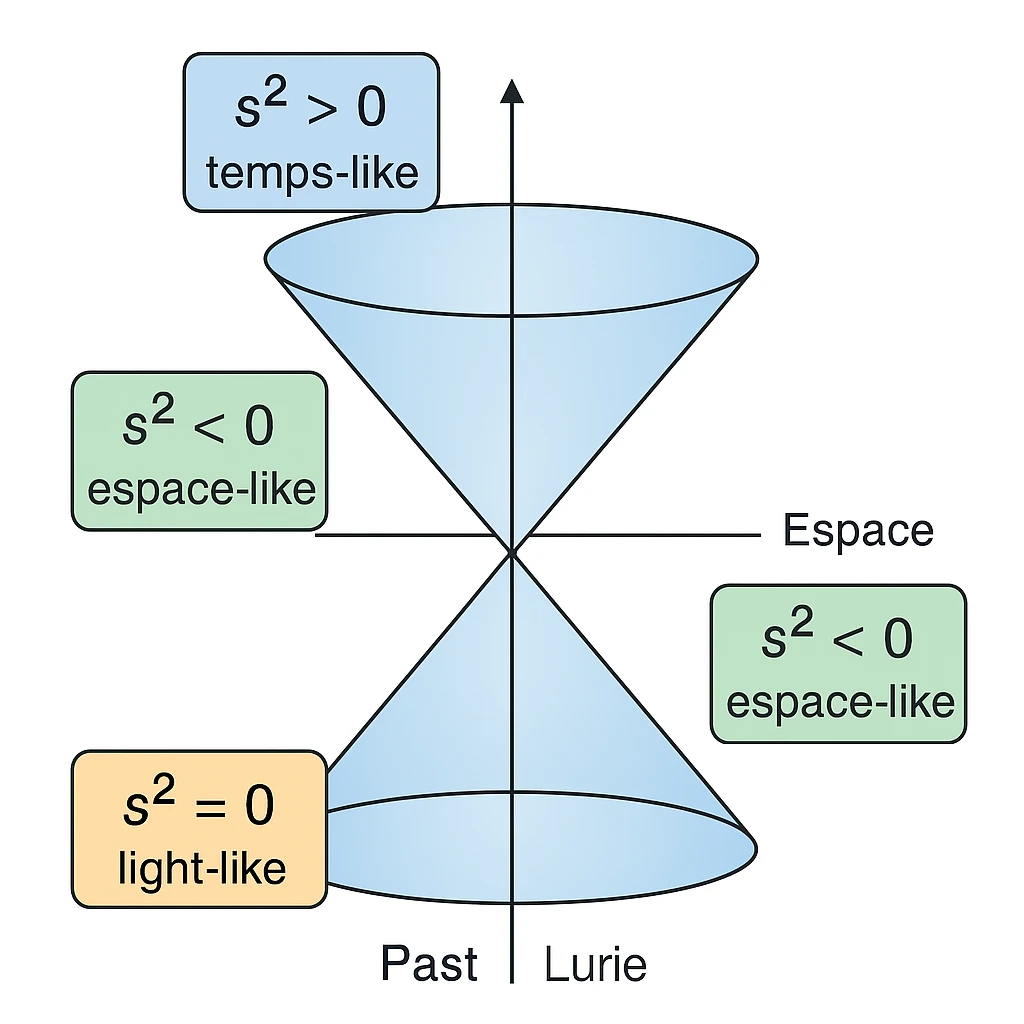
La relación \( s^2 = c^2 t^2 - x^2 - y^2 - z^2 \) es conocida como la métrica de Minkowski. Define un intervalo invariante entre dos eventos en el espacio-tiempo.
Aquí, \(c\) representa la velocidad de la luz, \(t\) el tiempo medido por un observador en reposo, y \((x, y, z)\) las coordenadas espaciales de los eventos. La invariancia de \(s^2\) implica que todos los observadores, independientemente de su movimiento relativo o posición, medirán el mismo intervalo cuatridimensional entre dos eventos.
Esta métrica muestra que el tiempo y el espacio no son entidades separadas: un cambio en las coordenadas espaciales resulta en un cambio efectivo en el tiempo percibido, un fenómeno conocido como dilatación temporal. Por ejemplo, un observador en movimiento rápido medirá un tiempo \(\Delta t\) más largo entre dos eventos que un observador en reposo.
Esta formalización matemática constituye la base de todos los experimentos modernos sobre la relatividad, ya sean relojes atómicos en movimiento o sistemas GPS que requieren corrección de efectos relativistas.
La dilatación del tiempo observada en partículas rápidas, o el enlentecimiento temporal cerca de un objeto masivo, confirma que la cuarta dimensión no es solo un concepto abstracto, sino una propiedad física medible. Los experimentos realizados con relojes atómicos en vuelo o en órbita demuestran la validez de las ecuaciones relativistas con una precisión > 10-15.
| Científico / Concepto | Contribución | Año | Referencia |
|---|---|---|---|
| Hermann Minkowski (1864-1909) | Introducción del espacio-tiempo como estructura geométrica | 1908 | Minkowski, Conferencia en Colonia (1908) |
| Albert Einstein (1879-1955) | Relatividad especial: tiempo vinculado al movimiento | 1905 | Einstein A., Annalen der Physik 1905 |
| Albert Einstein (1879-1955) | Relatividad general: curvatura del espacio-tiempo | 1915 | Einstein A., Sitzungsberichte der Preussischen Akademie 1915 |
| Arthur Eddington (1882-1944) | Observación de la deflexión de la luz > validación de la curvatura temporal | 1919 | Eddington A., Expedición de Sobral y Príncipe, 1919 |
| Hafele & Keating | Medición experimental de la dilatación temporal con relojes atómicos | 1971 | Hafele J., Keating R., Science 1972 |
Fuentes: Archivos de Albert Einstein, Nature, Science.