A geometria do tempo: explorar a quarta dimensão do Universo

Noção de tempo

Desde o início do século XX, a noção de tempo deixou de ser um simples parâmetro universal, presente desde sempre, para se tornar uma dimensão integrada na própria estrutura do Universo. A teoria da relatividade restrita, formulada em 1905 por Albert Einstein (1879-1955), mostrou que a duração medida depende do movimento relativo do observador. Em 1915, a relatividade geral introduziu a curvatura do espaço-tempo (estrutura quadridimensional que combina espaço e tempo) sob o efeito da massa e da energia.

Tempo e espaço unidos: uma unidade geométrica

O espaço-tempo (conjunto das três dimensões espaciais e do tempo, formando uma variedade quadridimensional) pode ser descrito como uma variedade de quatro dimensões onde os eventos possuem coordenadas \((x, y, z, ct)\). A métrica de Minkowski, que formaliza o intervalo espaço-temporal da relatividade restrita, foi formulada em 1908 por Hermann Minkowski (1864-1909).
Ela define o intervalo invariante: $$ \boxed{\color{blue}{\displaystyle s^2}} = (ct)^2 - x^2 - y^2 - z^2 $$
Esta relação mostra que o tempo e o espaço estão intimamente ligados, e que a geometria do tempo depende da velocidade do observador e da gravitação.

Por que vincular c e t nas coordenadas do espaço-tempo?

As coordenadas de um evento são frequentemente escritas como (x, y, z, ct) em vez de (x, y, z, t) para que o componente temporal ct tenha a mesma dimensão (comprimento) que as coordenadas espaciais.
Problema: x, y e z são expressos em metros, enquanto ���� é expresso em segundos → Impossível somá-los diretamente em uma norma ou distância.
Solução: Multiplicar ���� por ���� (velocidade da luz), que tem a unidade m/s: ��������[m]. Assim, ct está em metros, como x, y, z. Essa homogeneidade torna o intervalo de Minkowski, \( \boldsymbol{s^2} = (ct)^2 - x^2 - y^2 - z^2 \), mais compacto e permite representar o espaço e o tempo em um mesmo quadro geométrico de quatro dimensões.

A métrica de Minkowski e o espaço-tempo

Tipo de intervalo espaço-temporal

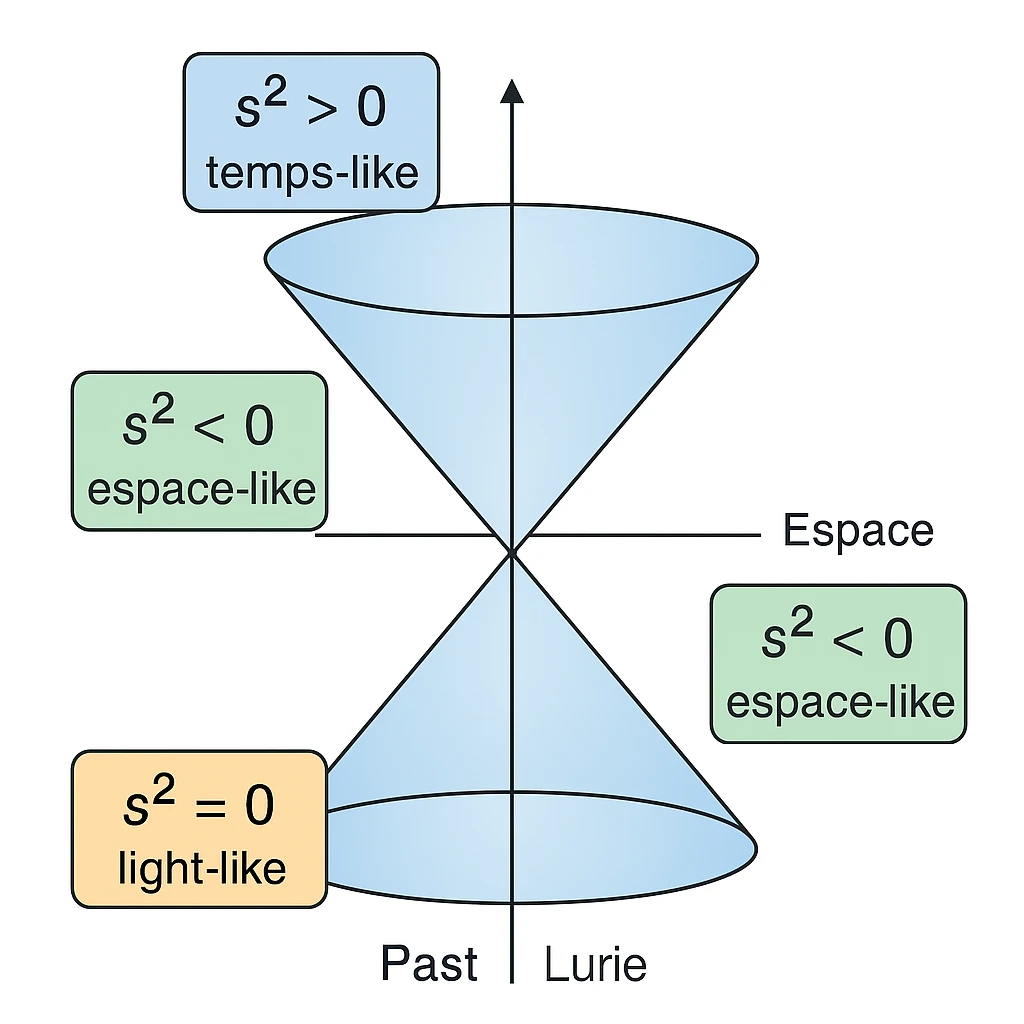
A relação \( s^2 = c^2 t^2 - x^2 - y^2 - z^2 \) é conhecida como a métrica de Minkowski. Ela define um intervalo invariante (distância quadridimensional entre dois eventos no espaço-tempo) entre dois eventos no espaço-tempo (combinação das três dimensões espaciais e do tempo).

Aqui, \(c\) representa a velocidade da luz, \(t\) o tempo medido por um observador em repouso, e \((x, y, z)\) as coordenadas espaciais dos eventos. A invariância de \(s^2\) implica que todos os observadores, independentemente de seu movimento relativo ou posição, medirão o mesmo intervalo quadridimensional entre dois eventos.

Essa métrica mostra que o tempo e o espaço não são entidades separadas: uma mudança nas coordenadas espaciais resulta em uma mudança efetiva no tempo percebido, um fenômeno conhecido como dilatação temporal (dilatação do tempo devido ao movimento relativo ou à gravitação). Por exemplo, um observador em movimento rápido medirá um tempo \(\Delta t\) mais longo entre dois eventos do que um observador em repouso.

Essa formalização matemática constitui a base de todos os experimentos modernos sobre a relatividade, sejam relógios atômicos em movimento ou sistemas GPS que requerem correção dos efeitos relativísticos.

Consequências físicas

A dilatação do tempo observada em partículas rápidas, ou o retardamento temporal perto de um objeto massivo, confirma que a quarta dimensão não é apenas um conceito abstrato, mas uma propriedade física mensurável. Os experimentos realizados com relógios atômicos em voo ou em órbita demonstram a validade das equações relativísticas com uma precisão > 10^-15.

Tabela resumo

• Fontes: Arquivos de Albert Einstein (nova janela), Nature (nova janela), Science (nova janela).